1.14 外積
定義 1.68 (外積)
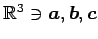 に対して,
外積(outer product)
またはベクトル積(vector product)は
に対して,
外積(outer product)
またはベクトル積(vector product)は
と表記する二項演算である.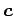 の長さは
の長さは
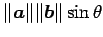 であり,
であり,
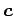 の向きは
の向きは 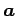 と
と 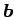 に右手系で直交する方向である.
に右手系で直交する方向である.
| (106) |
と表記する二項演算である.
注意 1.69 (外積の長さ)
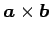 の長さは
の長さは  ,
,
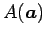 ,
,
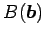 ,
,
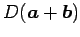 を頂点とする平行四辺形の面積である.
を頂点とする平行四辺形の面積である.
注意 1.70 (右手系)
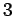 次元空間内の直交する座標軸
次元空間内の直交する座標軸 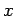 ,
, 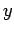 ,
, 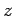 を考える.
軸のとり方は二通り存在する.
親指,人差指,中指を互いに直交するように曲げる.
このとき,
これらの指の向きをそれぞれ
を考える.
軸のとり方は二通り存在する.
親指,人差指,中指を互いに直交するように曲げる.
このとき,
これらの指の向きをそれぞれ
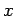 軸,
軸,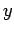 軸,
軸,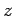 軸の向きとする.
右手の指に対応させるときと,
左手の指に対応させるときでは生成される座標軸は異なる.
それぞれ右手系,左手系と呼ぶ.
通常は右手系を使うことが多い.
軸の向きとする.
右手の指に対応させるときと,
左手の指に対応させるときでは生成される座標軸は異なる.
それぞれ右手系,左手系と呼ぶ.
通常は右手系を使うことが多い.
注意 1.71 (外積の向き)
外積
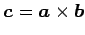 では
右手の親指,人差指,中指と
では
右手の親指,人差指,中指と 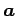 ,
, 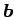 ,
, 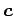 を
対応させる.
を
対応させる.
Kondo Koichi

平成17年9月15日