1.15 外積を成分で計算
定理 1.72 (外積の成分表示)
に対して,
が成り立つ.
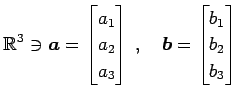 |
(107) |
に対して,
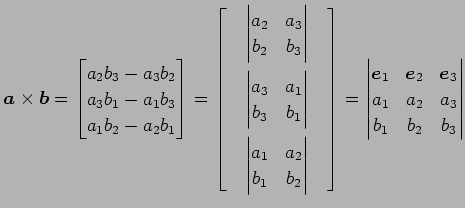 |
(108) |
が成り立つ.
問 1.73 (外積の成分表示)
これを示せ.
例 1.74 (外積の計算例)
![$ \vec{a}={[1\,\,2\,\,3]}^{T}$](img306.png) ,
,
![$ \vec{b}={[4\,\,5\,\,6]}^{T}$](img307.png) の外積は
の外積は
である.
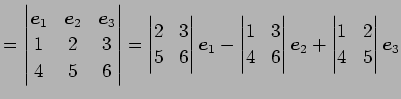 |
(109) | |
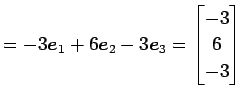 |
(110) |
である.
Kondo Koichi

平成17年9月15日