1.13 内積と面積
注意 1.65 (ベクトルの内積の図説)
ベクトル 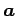 と
と 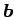 の成す角を
の成す角を 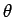 とするとき
とするとき
が成り立つ. すなわち,辺の長さが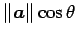 と
と
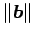 の長方形の面積を表す.
角度
の長方形の面積を表す.
角度 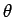 の値により面積は変化する.
の値により面積は変化する.
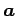 と
と 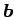 とが
同じ向きのとき,すなわち
とが
同じ向きのとき,すなわち 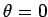 のときは,
面積は最大値をとり
のときは,
面積は最大値をとり
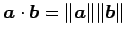 で与えられる.
で与えられる.
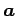 と
と 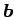 とが直交し
とが直交し
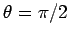 のときは,
面積は最小値をとり
のときは,
面積は最小値をとり
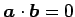 で与えられる.
で与えられる.
| (97) |
が成り立つ. すなわち,辺の長さが
定理 1.66 (平行四辺形の面積)
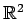 内の点
内の点 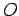 ,
,
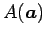 ,
,
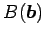 ,
,
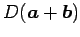 を考える.
このとき平行四辺形
を考える.
このとき平行四辺形 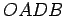 の面積は
の面積は
で与えられる.ただし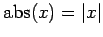 とする.
とする.
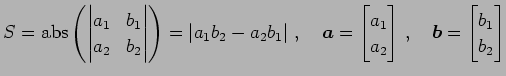 |
(98) |
で与えられる.ただし
問 1.67 (平行四辺形の面積)
これを証明せよ.
を得る.
が
を満すとする. このとき
が成り立つ.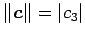 はベクトル
はベクトル 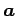 ,
,  が
なす平行四辺形の面積に等しい.
が
なす平行四辺形の面積に等しい.
(証明その1)
角度
![]() とする.
平行四辺形の面積は底辺の長さ
とする.
平行四辺形の面積は底辺の長さ
![]() と
高さ
と
高さ
![]() を掛けたものであるので,
これを計算すると
を掛けたものであるので,
これを計算すると
| (99) | ||
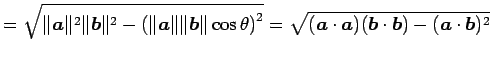 |
(100) | |
| (101) | ||
| (102) |
を得る.
(証明その2)
![]() のベクトル
のベクトル
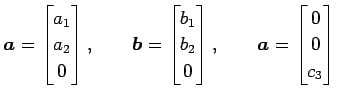 |
(103) |
が
| (104) |
を満すとする. このとき
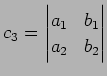 |
(105) |
が成り立つ.
Kondo Koichi

平成17年9月15日