1.12 ベクトルの直交
定義 1.62 (ベクトルの直交)
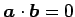 のとき
のとき 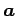 と
と 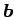 は
直交する(orthogonal)という.
このとき
は
直交する(orthogonal)という.
このとき
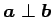 と表記する.
と表記する.
例 1.63 (ベクトルの直交の具体例)
を考える.このとき
が成り立つ.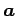 と
と 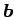 は互いに直交する.
は互いに直交する.
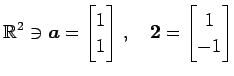 |
(93) |
を考える.このとき
| (94) |
が成り立つ.
例 1.64 (ベクトルの直交の具体例)
を考える.このとき に対して
に対して
が成り立つ. よって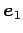 ,
,
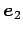 ,
,  ,
,
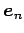 は
互いに直交する.
は
互いに直交する.
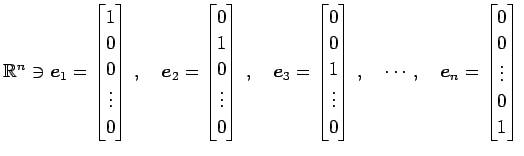 |
(95) |
を考える.このとき
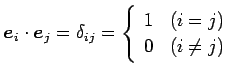 |
(96) |
が成り立つ. よって
Kondo Koichi

平成17年9月15日