1.7 直線の方程式
定義 1.31 (直線)
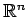 空間内の点
空間内の点 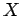 の位置ベクトルが
の位置ベクトルが
と表されるとき, 点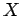 の軌跡を直線(line)という.
の軌跡を直線(line)という.
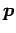 を方向ベクトル(tangent vector)という.
を方向ベクトル(tangent vector)という.
| (36) |
と表されるとき, 点
注意 1.32 (
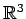 の直線の方程式)
直線
の直線の方程式)
直線
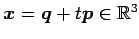 を考える.
ここで
を考える.
ここで
とおく.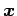 は点
は点
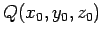 を通り
方向ベクトルが
を通り
方向ベクトルが 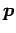 の直線である.
成分をまとめて書くと
の直線である.
成分をまとめて書くと
である. これを 直線の方程式のパラメータ表示と呼ぶことにする. また,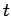 についてまとめると
直線の方程式は
についてまとめると
直線の方程式は
と表される. これを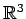 の直線の方程式の成分表示
である.
の直線の方程式の成分表示
である.
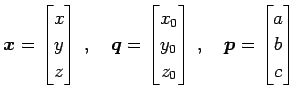 |
(37) |
とおく.
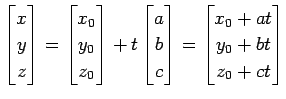 |
(38) |
である. これを 直線の方程式のパラメータ表示と呼ぶことにする. また,
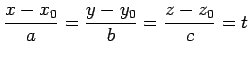 |
(39) |
と表される. これを
注意 1.33 (直線の方程式の成分表示)
直線の方程式
は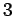 変数,
変数,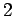 本の
連立方程式であることに注意する.
本の
連立方程式であることに注意する.
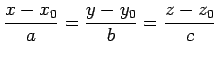 |
(40) |
は
問 1.34 (直線の方程式の成分表示)
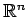 の直線の方程式の成分表示を求めよ.
の直線の方程式の成分表示を求めよ.
問 1.35 (
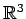 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 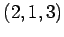 を通り
方向ベクトルが
を通り
方向ベクトルが
![$ {[-2\,\,3\,\,1]}^{T}$](img176.png) の
直線の方程式を求めよ.
の
直線の方程式を求めよ.
例 1.36 (
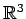 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 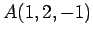 ,
,
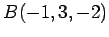 を通る直線の方程式を考える.
直線は点
を通る直線の方程式を考える.
直線は点  を通り,方向ベクトルは
を通り,方向ベクトルは
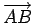 である.
すなわち,
である.
すなわち,
とおく. 直線の方程式のパラメータ表示は
である.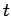 を消去して
直線の方程式の成分表示は
を消去して
直線の方程式の成分表示は
である.
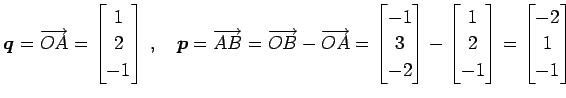 |
(41) |
とおく. 直線の方程式のパラメータ表示は
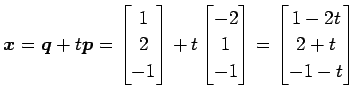 |
(42) |
である.
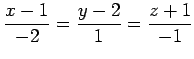 |
(43) |
である.
Kondo Koichi

平成17年9月15日