1.6 内分点
定理 1.24 (内分点)
点
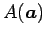 ,
,
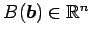 に対して
点
に対して
点
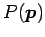 が
が
を満すとき,
が成り立つ.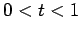 のとき点
のとき点 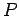 は点
は点  ,
,  の
内分点(internally dividing point)を表し,
の
内分点(internally dividing point)を表し,
 ,
, 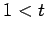 のとき
外分点(externally dividing point)を表す.
のとき
外分点(externally dividing point)を表す.
| (25) |
を満すとき,
| (26) |
が成り立つ.
注意 1.25 (内分点とパラメータ)
端点は
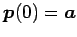 ,
,
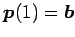 であり,
であり,
 ,
,  の中点は
の中点は
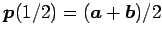 である.
である.
例 1.26 (内分点の具体例)
点 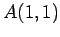 ,
,
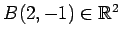 を考える.
このとき
を考える.
このとき
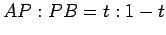 とする内分点
とする内分点
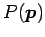 は
は
と与えられる. 点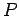 の座標を
の座標を 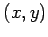 とする.このとき
とする.このとき
より
が成り立つ.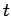 を消去すると
を消去すると
となる. この式は点 ,
,  を通る
を通る
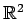 内の直線の方程式を表す.
内分点
内の直線の方程式を表す.
内分点 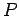 は直線上の点である.
は直線上の点である.
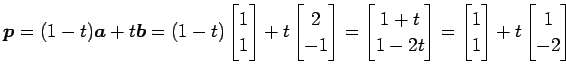 |
(27) |
と与えられる. 点
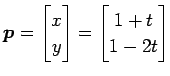 |
(28) |
より
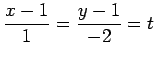 |
(29) |
が成り立つ.
| (30) |
となる. この式は点
問 1.27 (2 次元空間内の内分点)
点
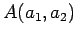 ,
,
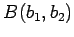 を
を
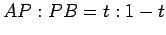 と
内分する点
と
内分する点 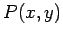 を求めよ.
また,点
を求めよ.
また,点  ,
,  を通る直線の方程式を求めよ.
を通る直線の方程式を求めよ.
例 1.28 (内分点の具体例)
点 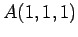 ,
,
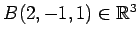 を考える.
このとき
を考える.
このとき
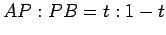 と内分する点
と内分する点
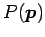 は
は
と与えられる.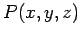 とすると
とすると
![$ \vec{p}={[x\,\,y\,\,z]}^{T}$](img152.png) より
より
が成り立つ. この式は点 ,
,  を通る
を通る
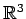 内の直線の方程式を表す.
内の直線の方程式を表す.
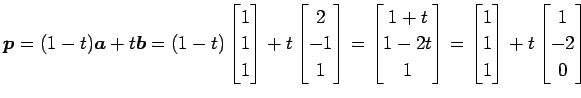 |
(31) |
と与えられる.
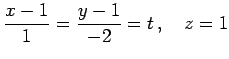 |
(32) |
が成り立つ. この式は点
定理 1.29 (3 次元空間内の内分点と直線の方程式)
点
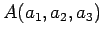 ,
,
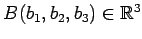 を
考える.
を
考える.
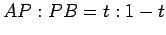 と内分する点を
と内分する点を
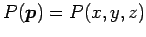 とする.
このとき
とする.
このとき
であり,
が成り立つ. 点 ,
,  を通る
を通る
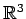 内の
直線の方程式は
内の
直線の方程式は
で与えられる.
| (33) |
であり,
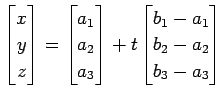 |
(34) |
が成り立つ. 点
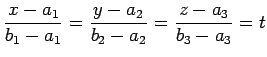 |
(35) |
で与えられる.
注意 1.30 (内分点,外分点が成す集合は 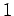 次元)
パラメータ
次元)
パラメータ 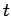 が一つ定まれば
が一つ定まれば
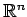 内の点が
内の点が
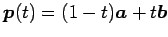 により
一つ定まる.
により
一つ定まる.
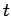 は
は
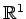 内の全ての点を動く.
よって
内の全ての点を動く.
よって
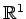 内の全ての点と直線
内の全ての点と直線
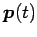 上の全ての点は
一対一対応する.
上の全ての点は
一対一対応する.
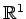 は
は 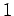 次元の空間であるので
直線
次元の空間であるので
直線
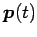 が成す集合もまた
が成す集合もまた 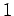 次元である.
次元である.
Kondo Koichi

平成17年9月15日