1.4 平行四辺形の面積
定理 1.17 (平行四辺形の面積)
点 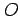 ,
,
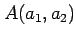 ,
,
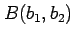 ,
,
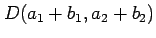 からなる平行四辺形
からなる平行四辺形 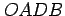 の面積は
の面積は
で与えられる.
とおく. すると,
と得られる.
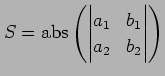 |
で与えられる.
(証明) まず,
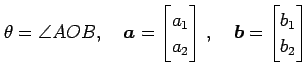 |
とおく. すると,
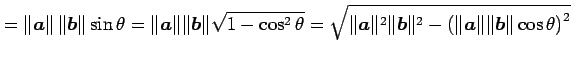 |
(1) | |
| (2) | ||
| (3) | ||
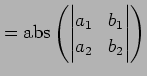 |
(4) |
と得られる.
Kondo Koichi

平成18年1月18日