1.3
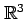 の直線と平面
の直線と平面
定義 1.9 (直線)
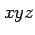 空間における直線は,
パラメータ
空間における直線は,
パラメータ 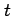 を用いてベクトルで表すと,
を用いてベクトルで表すと,
と書ける.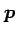 は方向ベクトルである.
成分で表すと,
は方向ベクトルである.
成分で表すと,
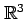 の直線の方程式
の直線の方程式
が得られる.
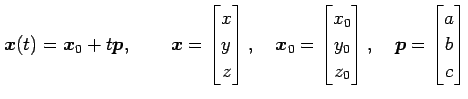 |
と書ける.
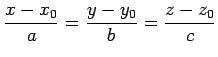 |
が得られる.
定義 1.10 (平面の方程式)
 空間内の平面の方程式は
空間内の平面の方程式は
と表される.ベクトルで表記すると
となる.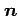 を法線ベクトルという.
を法線ベクトルという.
と表される.ベクトルで表記すると
となる.
注意 1.11 (平面,直線)
 ,
, 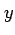 ,
, 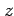 に関する非同次 1 次方程式の一般形は
に関する非同次 1 次方程式の一般形は
である.この方程式は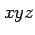 空間内の
法線ベクトルが
空間内の
法線ベクトルが
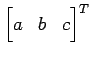 で点
で点
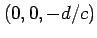 を通る平面を表す.
非同次 1 次方程式を 2 本の方程式で連立すると
を通る平面を表す.
非同次 1 次方程式を 2 本の方程式で連立すると
である.方程式のそれぞれは法線ベクトルが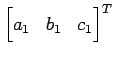 と
と
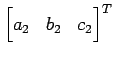 の
平面を表す.
よって,
この連立方程式の解集合は,
2 つの平面の共有点の集合である直線となる.
の
平面を表す.
よって,
この連立方程式の解集合は,
2 つの平面の共有点の集合である直線となる.
である.この方程式は
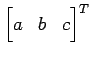 で点
で点
である.方程式のそれぞれは法線ベクトルが
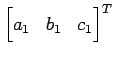 と
と
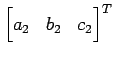 の
平面を表す.
よって,
この連立方程式の解集合は,
2 つの平面の共有点の集合である直線となる.
の
平面を表す.
よって,
この連立方程式の解集合は,
2 つの平面の共有点の集合である直線となる.
例 1.12 (直線)
2 点 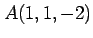 ,
, 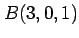 を通る
を通る
 空間内の直線を考える.
この直線の方向ベクトルは
空間内の直線を考える.
この直線の方向ベクトルは
である.直線のパラメータ表示は
となる.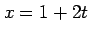 ,
, 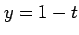 ,
, 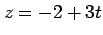 で
で 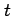 を消去すると,
直線の方程式
を消去すると,
直線の方程式
を得る.
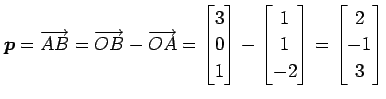 |
である.直線のパラメータ表示は
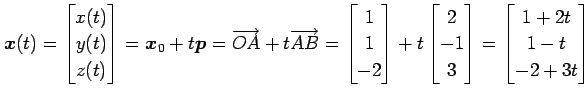 |
となる.
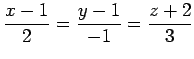 |
を得る.
例 1.13 (平面)
3 点 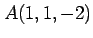 ,
, 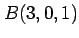 ,
, 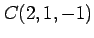 を通る
を通る
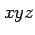 空間内の平面を考える.
法線ベクトルは
空間内の平面を考える.
法線ベクトルは
であり,点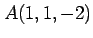 を通るので,
を通るので,
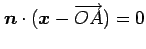 より
平面の方程式
より
平面の方程式
を得る.一般形で書けば
となる.さらに変形して
とする. 平面と 軸,
軸,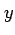 軸,
軸,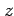 軸の交点はそれぞれ
軸の交点はそれぞれ
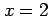 ,
, 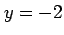 ,
, 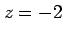 である.
である.
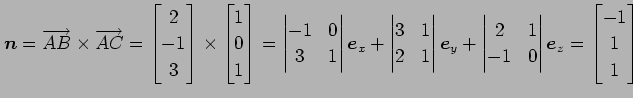 |
であり,点
を得る.一般形で書けば
となる.さらに変形して
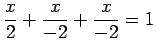 |
とする. 平面と
例 1.14 (平面)
3 点 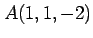 ,
, 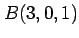 ,
, 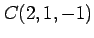 を通る
を通る
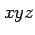 空間内の平面を考える.
平面の方程式の一般形は
空間内の平面を考える.
平面の方程式の一般形は
であるから,これに各点の座標を代入すると 連立方程式
を得る.この方程式の解は
である.よって平面の方程式は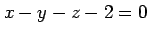 となる.
となる.
であるから,これに各点の座標を代入すると 連立方程式
を得る.この方程式の解は
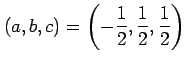 |
である.よって平面の方程式は
例 1.15 (直線)
連立方程式
で定まる直線を考える. この直線は 2 つの平面の共有点である. 第 2 式から第 1 式を引いて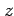 を消去すると
を消去すると
であり,第 1 式と第 2 式を足して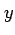 を消去すると
を消去すると
となる. これらより
を得る. 直線は点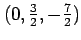 を通り,
方向ベクトル
を通り,
方向ベクトル
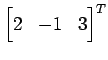 の
直線である.
また,パラメータ表示すると
の
直線である.
また,パラメータ表示すると
である.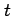 は任意であるから,
は任意であるから,
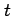 を
を
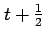 と置き換えると,
と置き換えると,
となり,式が簡単となる. このとき平面の方程式は
となる.直線は点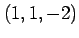 も通る.
も通る.
で定まる直線を考える. この直線は 2 つの平面の共有点である. 第 2 式から第 1 式を引いて
であり,第 1 式と第 2 式を足して
となる. これらより
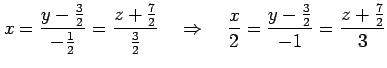 |
を得る. 直線は点
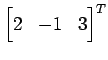 の
直線である.
また,パラメータ表示すると
の
直線である.
また,パラメータ表示すると
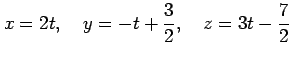 |
である.
となり,式が簡単となる. このとき平面の方程式は
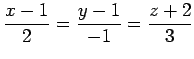 |
となる.直線は点
例 1.16 (直線)
連立方程式
で定まる直線を考える. この直線は 2 つの平面の解集合であるから, 連立方程式
を解く. 拡大係数行列を簡約化すると
となる. このとき方程式は
と変形される. 階数が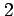 であるから,任意定数は 1 個であるので,
任意定数
であるから,任意定数は 1 個であるので,
任意定数 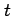 を
を 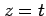 とおくと,
とおくと,
を得る.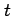 は任意定数であるから,
は任意定数であるから,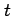 を
を 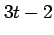 と置き換えると,
と置き換えると,
を得る.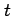 を消去すると平面の方程式
を消去すると平面の方程式
を得る.
で定まる直線を考える. この直線は 2 つの平面の解集合であるから, 連立方程式
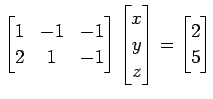 |
を解く. 拡大係数行列を簡約化すると
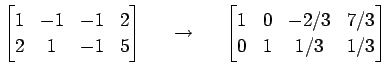 |
となる. このとき方程式は
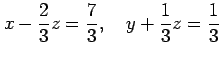 |
と変形される. 階数が
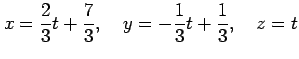 |
を得る.
を得る.
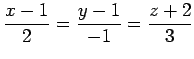 |
を得る.
Kondo Koichi

平成18年1月18日