3.8 斜交座標への置換積分
例 3.43 (多重積分の変数変換)
多重積分
を求める. 積分変数を
とおく.この逆は
である. このとき領域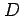 を
を 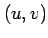 で表すと
で表すと
となる. 座標変換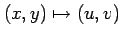 のヤコビアンは
のヤコビアンは
である.これらより,
を得る.
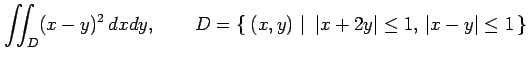 |
を求める. 積分変数を
とおく.この逆は
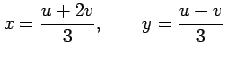 |
である. このとき領域
となる. 座標変換
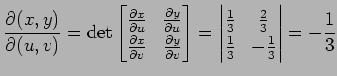 |
である.これらより,
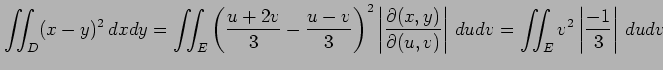 |
||
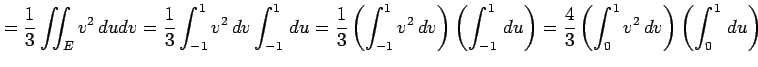 |
||
![$\displaystyle = \frac{4}{3} \left[\vrule height1.5em width0em depth0.1em\,{\fra...
...times\left[\vrule height1.5em width0em depth0.1em\,{u}\,\right]_0^1=\frac{4}{9}$](img1479.png) |
を得る.
注意 3.44 (面素)
置換積分により面素は
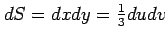 と変換される.
直交座標
と変換される.
直交座標 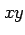 では微小面積は,
辺の長さが
では微小面積は,
辺の長さが 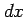 ,
, 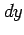 の長方形の面積
の長方形の面積 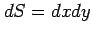 である.
これに対して斜交座標
である.
これに対して斜交座標 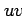 の微小面積は,
辺の長さが
の微小面積は,
辺の長さが 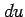 ,
, 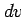 の平行四辺形の面積
の平行四辺形の面積
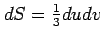 である.
これを示す.
である.
これを示す.
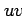 座標の基底は
座標の基底は
であり, 点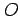 ,
,
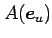 ,
,
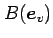 ,
,
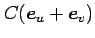 から
なる平行四辺形の面積は
から
なる平行四辺形の面積は
である. ここで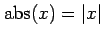 とおいた.
面素
とおいた.
面素 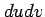 は辺の長さが
は辺の長さが 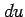 ,
, 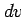 で
平行四辺形
で
平行四辺形 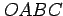 と相似な図形であるから,
面素
と相似な図形であるから,
面素 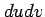 の面積
の面積 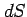 は
は
と得られる.
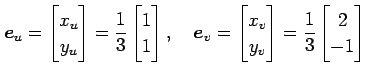 |
であり, 点
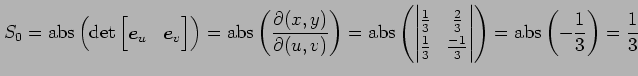 |
である. ここで
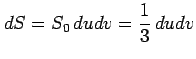 |
と得られる.
問 3.45 (多重積分の変数変換)
領域 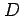 を下図 (b) のように 4 つに分割し多重積分を求めよ.
を下図 (b) のように 4 つに分割し多重積分を求めよ.
![\includegraphics[width=0.4\textwidth]{chikan-shakou-D.eps}](img1495.png) |
![\includegraphics[width=0.4\textwidth]{chikan-shakou-Dx.eps}](img1496.png) |
| (a) 領域 |
(b) 領域 |
![\includegraphics[width=0.4\textwidth]{chikan-shakou-uv.eps}](img1497.png) |
![\includegraphics[width=0.4\textwidth]{chikan-shakou-E.eps}](img1498.png) |
| (c) |
(d) 領域 |
![\includegraphics[width=0.4\textwidth]{chikan-shakou-I.eps}](img1499.png) |
![\includegraphics[width=0.4\textwidth]{chikan-shakou-Iuv.eps}](img1500.png) |
| (e) |
(f) |
Kondo Koichi

平成18年1月18日