5.19 テイラー級数を用いた関数の極限の計算
関数
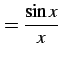 |
(789) |
の
| (790) |
として計算する. まず分子である
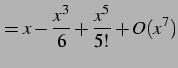 |
(791) |
となる. 次に分子
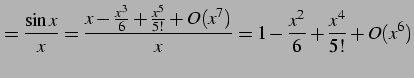 |
(792) |
を得る. もとの関数とテイラー級数で表わした関数とは等価なものである. よって
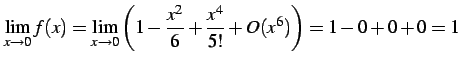 |
(793) |
を得る. 関数
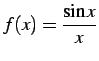 はもともと点
はもともと点
問 5.47 (極限の計算)
極限
を求めよ.
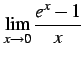 |
(794) |
を求めよ.
例 5.48 (テイラー展開を用いた極限の計算の例)
関数
に対して極限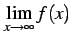 を考える.
このとき
を考える.
このとき
として極限を求める. しかしながら, 巾級数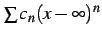 は存在しない.
そこで変数を
は存在しない.
そこで変数を 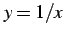 と導入する.
すると極限は
と導入する.
すると極限は
と表わされる.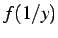 を計算すると
を計算すると
となる.まず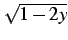 をテイラー展開すると
をテイラー展開すると
を得る. これを用いて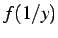 のテイラー展開を求めると
のテイラー展開を求めると
となる.よって極限は
と得られる.
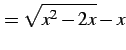 |
(795) |
に対して極限
| (796) |
として極限を求める. しかしながら, 巾級数
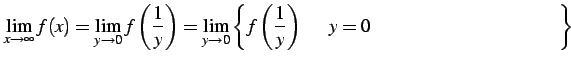 |
(797) |
と表わされる.
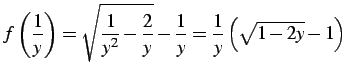 |
(798) |
となる.まず
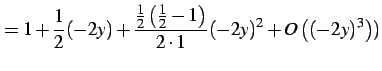 |
(799) | |
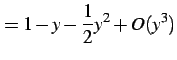 |
(800) |
を得る. これを用いて
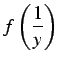 |
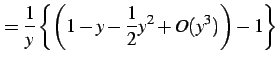 |
(801) |
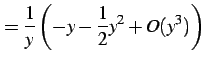 |
(802) | |
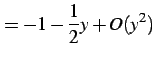 |
(803) |
となる.よって極限は
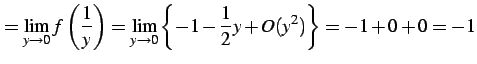 |
(804) |
と得られる.
Kondo Koichi

平成17年8月31日