5.14 項別積分
関数
![]() を考える.
を考える.
![]() のテイラー級数を求める.
このとき
のテイラー級数を求める.
このとき
![]() の計算は面倒であるので
別の方法を考える.
そこで次のような項別積分を用いて
テイラー級数を求める.
まず
の計算は面倒であるので
別の方法を考える.
そこで次のような項別積分を用いて
テイラー級数を求める.
まず ![]() の導関数は
の導関数は
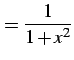 |
(716) |
である. これをテイラー級数で表わす. そのためまず
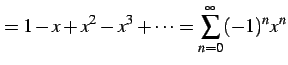 |
(717) |
を用意する.
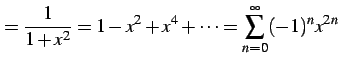 |
(718) |
を得る. 両辺を不定積分をすると
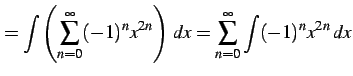 |
(719) | |
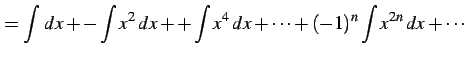 |
(720) | |
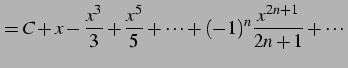 |
(721) | |
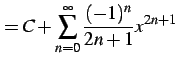 |
(722) | |
| (723) | ||
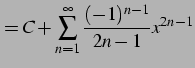 |
(724) |
を得る. 定数項
| (725) | ||
| (726) |
を得る. 以上より
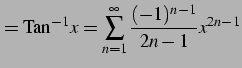 |
(727) |
が求まる.
Kondo Koichi

平成17年8月31日