3.15 高階導関数
定義 3.32 (高階導関数)
関数 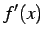 が微分可能のとき,
が微分可能のとき,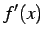 の導関数
の導関数
を2 階導関数(second order derivative)という. このとき は
2 回微分可能(two times differentiable)と呼ぶ.
同様に
は
2 回微分可能(two times differentiable)と呼ぶ.
同様に  を
を 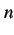 回繰り返し微分した関数を
回繰り返し微分した関数を
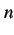 階導関数(
階導関数(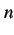 -th order derivative)といい,
-th order derivative)といい,
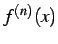 と書き表わす.
関数
と書き表わす.
関数
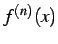 は
は
と再帰的に定義する. ただし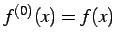 とする.
とする.
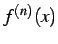 が存在するとき
が存在するとき  は
は
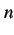 回微分可能(
回微分可能(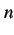 times differentiable)という.
times differentiable)という.
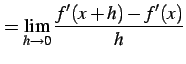 |
(321) |
を2 階導関数(second order derivative)という. このとき
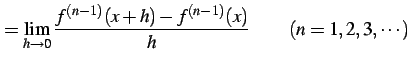 |
(322) |
と再帰的に定義する. ただし
注意 3.33 (高階導関数)
高階導関数
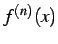 は関数
は関数 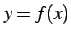 に
に 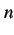 回
微分演算
回
微分演算
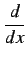 を作用させたものであるから,
記号の表記は次のように行う:
を作用させたものであるから,
記号の表記は次のように行う:
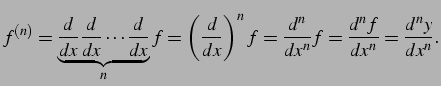 |
(323) |
例 3.34 (高階導関数の計算例)
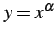 の高階導関数を求める.
の高階導関数を求める.
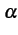 が自然数ではないとき,
が自然数ではないとき,
を得る. よって一般的に
と表される.
| (324) | ||
| (325) | ||
| (326) | ||
| (327) | ||
| (328) | ||
を得る. よって一般的に
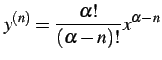 |
(329) |
と表される.
定義 3.35 (階乗の拡張)
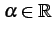 に対して
に対して
と定義する.
| (330) |
と定義する.
例 3.36 (高階導関数の計算例)
自然数 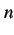 とする.
とする.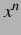 の高階導関数は
の高階導関数は
より,一般的に
と表される.
| (331) | ||
| (332) | ||
| (333) | ||
| (334) | ||
| (335) | ||
| (336) | ||
| (337) | ||
| (338) | ||
より,一般的に
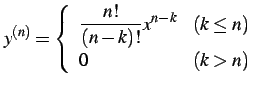 |
(339) |
と表される.
例 3.37 (高階導関数の計算例)
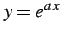 の高階導関数を求める.
合成関数の微分を繰り返して
の高階導関数を求める.
合成関数の微分を繰り返して
を得る.
| (340) | ||
| (341) | ||
| (342) | ||
| (343) | ||
| (344) |
を得る.
例 3.38 (高階導関数の計算例)
| (345) | ||
| (346) | ||
| (347) | ||
| (348) | ||
| (349) | ||
| (350) | ||
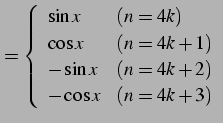 |
(351) | |
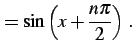 |
(352) |
問 3.39 (高階導関数の例)
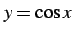 ,
, 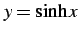 ,
, 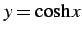 の
の 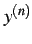 を求めよ.
を求めよ.
例 3.40 (高階導関数の計算例)
| (353) | ||
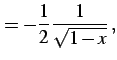 |
(354) | |
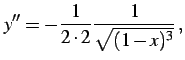 |
(355) | |
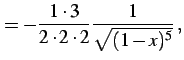 |
(356) | |
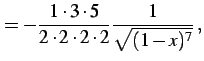 |
(357) | |
| (358) | ||
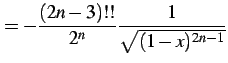 |
(359) |
定義 3.41 (階乗の拡張)
整数 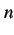 に対して
に対して 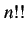 を
を
と定義する. すなわち奇数,偶数に対しては
と表される.
| (360) |
と定義する. すなわち奇数,偶数に対しては
| (361) | ||
| (362) |
と表される.
問 3.42 (高階導関数)
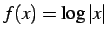 の高階導関数を求めよ.
の高階導関数を求めよ.
Kondo Koichi

平成17年8月31日