3.14 逆双曲線関数の微分
定理 3.30 (逆双曲線関数の微分)
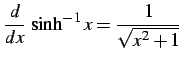 |
(309) |
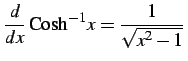 |
(310) |
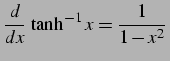 |
(311) |
問 3.31
これを示せ.
である.ここで を
を 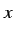 の関数で表わす.
の関数で表わす.
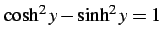 より
より
である.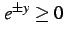 であり
であり
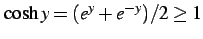 となることに考慮すると,
複合は正のみが採用される.
よって
となることに考慮すると,
複合は正のみが採用される.
よって
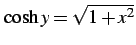 となる.
以上より
となる.
以上より
を得る.
となる.ここで を
を 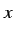 の関数で表わす.
の関数で表わす.
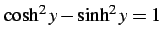 より
より
である.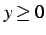 のとき
のとき
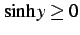 であるから
複合は正を採用する.よって
であるから
複合は正を採用する.よって
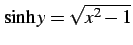 となる.
以上より
となる.
以上より
を得る.
となる.よって
を得る.
![]() とおく.このとき逆関数とその微分は
とおく.このとき逆関数とその微分は
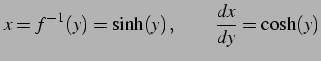 |
(312) |
である.ここで
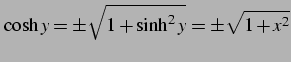 |
(313) |
である.
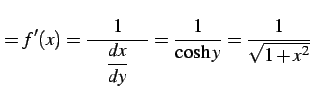 |
(314) |
を得る.
次に
![]() とおく.
このとき逆関数とその微分は
とおく.
このとき逆関数とその微分は
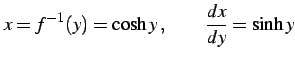 |
(315) |
となる.ここで
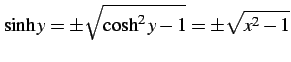 |
(316) |
である.
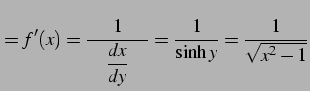 |
(317) |
を得る.
最後に
![]() とおく.この逆関数とその微分は
とおく.この逆関数とその微分は
| (318) | ||
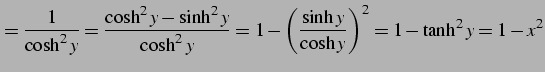 |
(319) |
となる.よって
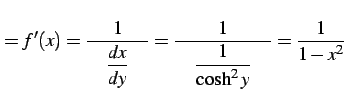 |
(320) |
を得る.
Kondo Koichi

平成17年8月31日