3.13 双曲線関数の微分
定理 3.28 (双曲線関数の微分)
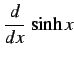 |
(300) | |
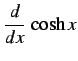 |
(301) | |
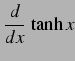 |
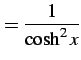 |
(302) |
問 3.29
これを示せ.
を得る.次に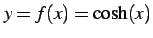 とおく.
このとき
とおく.
このとき
を得る. 最後に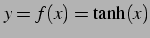 とおく.
このとき
とおく.
このとき
を得る.
![]() とおく.
このとき
とおく.
このとき
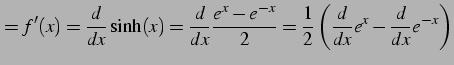 |
(303) | |
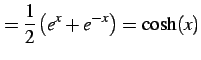 |
(304) |
を得る.次に
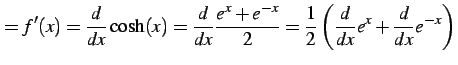 |
(305) | |
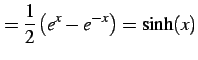 |
(306) |
を得る. 最後に
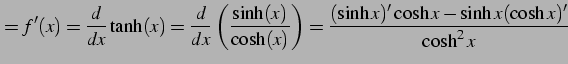 |
(307) | |
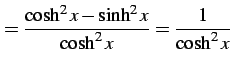 |
(308) |
を得る.
Kondo Koichi

平成17年8月31日