3.2 導関数
定義 3.6 (導関数)
関数 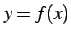 が連続関数であり,
定義域内の任意の点において微分可能であるとする.
このとき関数
が連続関数であり,
定義域内の任意の点において微分可能であるとする.
このとき関数
が存在する.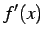 を
を  の
導関数(derived function, derivative)と呼ぶ.
導関数はまた
の
導関数(derived function, derivative)と呼ぶ.
導関数はまた
という表記も用いる.
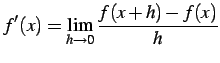 |
(199) |
が存在する.
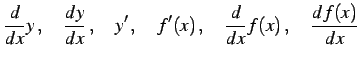 |
(200) |
という表記も用いる.
例 3.7 (導関数の計算例)
関数 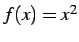 の導関数を求める.
まず
の導関数を求める.
まず
とおく.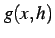 を計算すると
を計算すると
を得る. これより
となる. 極限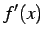 は
は
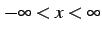 の任意の点において有限確定である.
よって導関数
の任意の点において有限確定である.
よって導関数 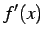 が存在し
が存在し 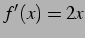 が求まる.
が求まる.
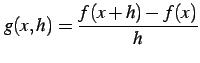 |
(201) |
とおく.
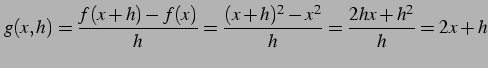 |
(202) |
を得る. これより
| (203) |
となる. 極限
Kondo Koichi

平成17年8月31日