2.29 みかけ上の不連続点
例 2.91 (不連続点の除去の具体例)
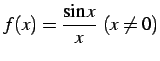 は
は 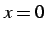 において
不連続である.なぜなら
において
不連続である.なぜなら 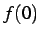 が定義されていないからである.
しかし
が定義されていないからである.
しかし  を
を
と定義すると は
は 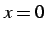 において連続となる.
なぜなら
において連続となる.
なぜなら
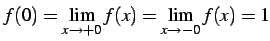 が
成立するからである.
再定義することにより不連続な点
が
成立するからである.
再定義することにより不連続な点 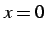 は取り除かれた.
は取り除かれた.
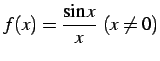 は
は ![$\displaystyle f(x)=\left\{ \begin{array}{cc} \displaystyle{\frac{\sin x}{x}} & (x\neq 0)\\ [1em] 1 & (x=0) \end{array} \right.$](img519.png) |
(172) |
と定義すると
例 2.92 (不連続点を除去できない具体例)
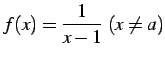 は点
は点 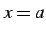 において不連続である.
点
において不連続である.
点 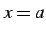 における値を
における値を 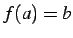 と定義することにする.
うまく
と定義することにする.
うまく 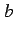 を定めることにより不連続点は取り除くことができるであろうか.
を定めることにより不連続点は取り除くことができるであろうか.
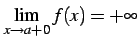 ,
,
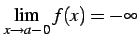 であるので,
点
であるので,
点 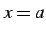 の左右で極限がことなる.よってどのように
の左右で極限がことなる.よってどのように 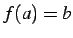 を定めても
不連続な点を取り除くことはできない.
を定めても
不連続な点を取り除くことはできない.
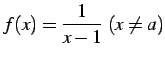 は点
は点
例 2.93 (不連続点の除去の具体例)
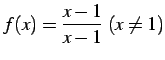 を考える.
を考える.
 は点
は点 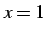 において不連続である.
しかし
において不連続である.
しかし  は分子分母が等しいので,
は分子分母が等しいので, 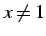 となる点において
となる点において
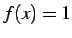 である.よって
である.よって
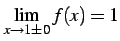 となる.
ゆえに点
となる.
ゆえに点 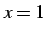 の値を
の値を
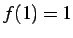 と定義すれば不連続点は取り除かれる.
結局,点
と定義すれば不連続点は取り除かれる.
結局,点 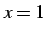 はみかけ上の不連続点であり本質的な不連続点ではない.
はみかけ上の不連続点であり本質的な不連続点ではない.
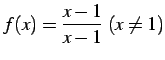 を考える.
を考える.
問 2.94 (不連続点の除去の例)
次の関数を 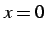 で連続となるように
で連続となるように 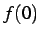 の値を定義せよ.
の値を定義せよ.
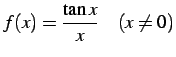 |
(173) | |
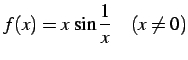 |
(174) | |
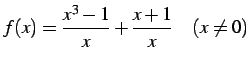 |
(175) |
Kondo Koichi

平成17年8月31日