2.28 連続と不連続
定義 2.88 (関数の連続性)
次の条件を満たすとき,関数  は点
は点 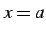 において
連続(continuous)であるという.
において
連続(continuous)であるという.
- (i)
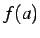 が定義されている.
が定義されている.
- (ii)
-
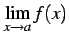 が存在する.
が存在する.
すなわち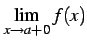 と
と
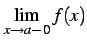 が存在し,それらの値が等しい.
が存在し,それらの値が等しい.
- (iii)
-
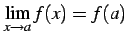 が成立する.
が成立する.
すなわち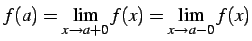 が
成立する.
が
成立する.
例 2.89 (連続な点の具体例)
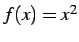 は
は 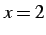 において連続である.
なぜなら
において連続である.
なぜなら
が成り立つからである.
| (171) |
が成り立つからである.
例 2.90 (不連続な点の具体例)
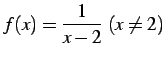 は
は
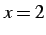 において不連続である.
なぜなら
において不連続である.
なぜなら 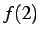 は定義されていない.
さらには
は定義されていない.
さらには
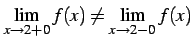 となるからである.
となるからである.
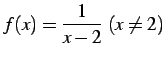 は
は
Kondo Koichi

平成17年8月31日