2.27 関数の極限の計算
公式 2.85 (ネピア数)
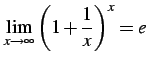 |
(162) |
公式 2.86 (sinc関数)
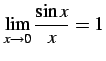 |
(163) |
問 2.87 (関数の極限の計算)
| (164) |
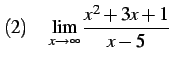 |
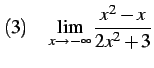 |
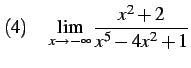 |
(165) | |||
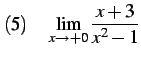 |
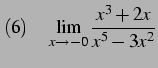 |
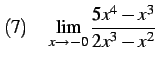 |
(166) | |||
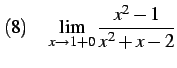 |
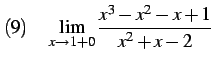 |
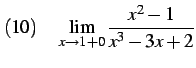 |
(167) | |||
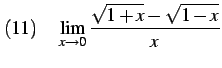 |
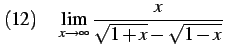 |
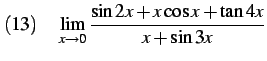 |
(168) | |||
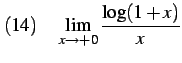 |
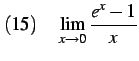 |
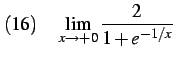 |
(169) | |||
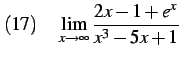 |
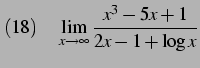 |
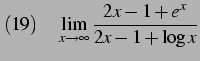 |
(170) |
Kondo Koichi

平成17年8月31日