2.25 関数の極限の性質
定理 2.78 (関数の極限に関する性質)
関数  ,
, 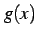 に関して極限
に関して極限
が存在するならば,
が成り立つ. ただし,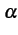 ,
, 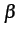 は定数である.
は定数である.
| (147) |
が存在するならば,
| (148) | ||
| (149) | ||
| (150) | ||
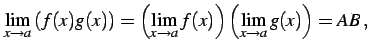 |
(151) | |
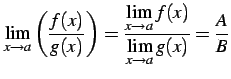 |
(152) |
が成り立つ. ただし,
例 2.79 (関数の極限の計算例)
| (153) | ||
| (154) | ||
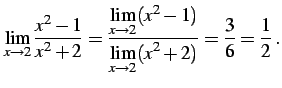 |
(155) |
Kondo Koichi

平成17年8月31日