6.11 定積分の性質
定理 6.38 (定積分の性質)
定積分は次の性質をもつ:
- (1)
-
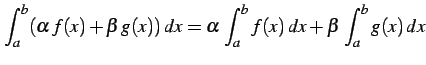 .
.
- (2)
-
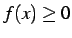
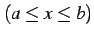 のとき
のとき
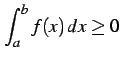 .
.
- (3)
-
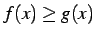
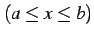 のとき
のとき
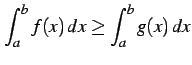 .
.
- (4)
-
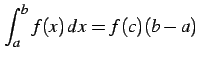 ,
,
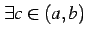 .
.
- (5)
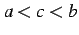 のとき
のとき
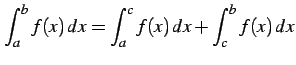 .
.
- (6)
-
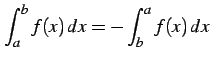 .
.
- (7)
-
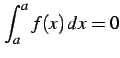 .
.
Kondo Koichi

平成17年8月31日