6.10 定積分
定義 6.35 (定積分)
有限区間 ![$ [a,b]$](img2002.png) において関数
において関数  は連続とする.
区間
は連続とする.
区間 ![$ [a,b]$](img2002.png) を
を
のように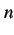 個の領域に分割する.
このとき面積
個の領域に分割する.
このとき面積
を考える. 極限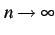 のもと
面積
のもと
面積 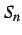 の極限が存在するとき,
この極限を
の極限が存在するとき,
この極限を
と書き, 関数 の
の 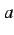 から
から 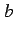 までの
定積分(definite integral)という.
このとき
までの
定積分(definite integral)という.
このとき
 は積分可能であるという.
区間
は積分可能であるという.
区間 ![$ [a,b]$](img2002.png) を積分区間という.
を積分区間という.
| (1031) |
のように
![$\displaystyle = \sum_{k=1}^{n} f(\xi_{k})\Delta x_{k}\,,\quad \xi_{k}\in I_{k}=[x_{k}, x_{k-1}]\,,\quad \Delta x_{k}=x_{k}-x_{k-1}$](img2004.png) |
(1032) |
を考える. 極限
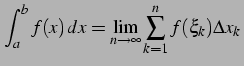 |
(1033) |
と書き, 関数
注意 6.36 (定積分の意味)
区間 ![$ [a,b]$](img2002.png) において
において 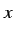 軸と
軸と 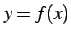 とで囲まれた領域の
符合付き面積である.
とで囲まれた領域の
符合付き面積である.
例 6.37 (定積分の具体例)
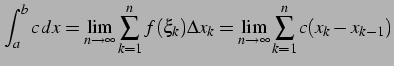 |
(1034) | |
| (1035) | ||
| (1036) |
Kondo Koichi

平成17年8月31日