12 直交変換

定義 2.55 (直交変換)   線形変換 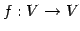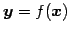$f:V\to V$; $\vec{y}=f(\vec{x})$ が

$$\Vert f(\vec{x})\Vert=\Vert\vec{x}\Vert$$

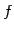をみたすとき， $f$ を直交変換（orthogonal transformation）という．

注意 2.56 (直交変換のノルムの不変性)   ベクトル 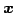$\vec{x}$ の長さと直交変換で写されたベクトル $\vec{y}$ の 長さは等しい．

定義 2.57 (直交変換の内積の不変性)   線形変換 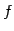$f$ が直交変換であるための必用十分条件は

$$(f(\vec{x}),f(\vec{x}'))=(\vec{x},\vec{x}'), \qquad \forall \vec{x},\vec{x}'\in V$$

である．

（証明）    

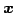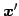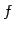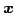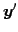定理 2.58 (直交変換の角の不変性)   ベクトル $\vec{x}$, $\vec{x}'$ を直交変換 $f$ に写したベクトルを $\vec{y}$, $\vec{y}'$ とする． このとき，$\vec{x}$, $\vec{x}'$ のなす角と $\vec{y}$, $\vec{y}'$ のなす角とは等しい．

注意 2.59 (合同変換)   直交変換は合同変換のひとつである． 合同変換（congruent transformation）とは， 長さと角を不変に保つ変換のことをいう． 合同変換で写される図形は，変換前の図形と後の図形とは合同となる． また，角を不変に保ち，長さはある定数倍になる変換のことを 相似変換（similarity transformation）という． 角を不変に保つ変換を等角変換という．

定理 2.60 (直交変換と直交行列)   直交変換の表現行列は直交行列である．

（証明）     （十分） $A$ を直交行列とする．

$$\vec{y}=A\vec{x}, \quad \vec{y}'=A\vec{x}$$

とおく．このとき

$$(f(\vec{x}),f(\vec{x}'))= (\vec{y},\vec{y}')= (A\vec{x},A\vec{x}'... ...x}'= {\vec{x}}^{T}({A}^{T}A)\vec{x}'= {\vec{x}}^{T}E\vec{x}= (\vec{x},\vec{x}')$$

をみたす．

Kondo Koichi
Created at 2004/12/13