Next: 12 直交変換 Up: 2 線形写像 Previous: 10 正則変換 Contents
11 直交行列
定義 2.47 (直交行列)
正方行列 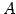 が
が
をみたすとき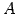 を
直交行列(orthogonal matrix)という.
を
直交行列(orthogonal matrix)という.
をみたすとき
定理 2.48 (直交行列の行列式)
直交行列の行列式は
である.
となるので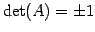 を得る.
を得る.
である.
(証明)
![]() より,両辺の行列式をとると
より,両辺の行列式をとると
となるので
定理 2.49 (直交行列の正則性)
直交行列は正則である.
(証明)
![]() であるから.
であるから.
定理 2.50 (直交行列の逆行列)
直交行列の逆行列は
である.
を得る.
である.
(証明)
![]() は正則であるか
は正則であるか ![]() を
を
![]() に左から掛けると
に左から掛けると
を得る.
定理 2.51 (直交行列の積)
直交行列の積もまた直交行列である.
(証明)
定理 2.52 (直交行列と正規直交系)
直交行列の列ベクトルまたは行ベクトルは正規直交系である.
とおく.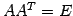 より,
より,
となるので,
を得る.
(証明)
直交行列 ![]() を列ベクトル
を列ベクトル
とおく.
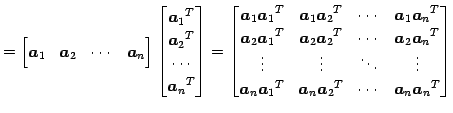 |
||
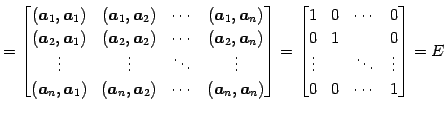 |
となるので,
を得る.
例 2.53 (直交行列の具体例)
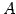 :
: 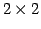 の直交変換は
の直交変換は
のみである.
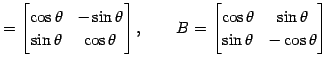 |
のみである.
問 2.54 (直交行列)
行列
が直交行列となるように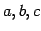 を定めよ.
を定めよ.
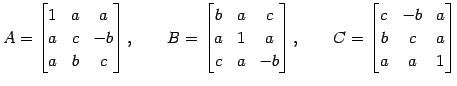 |
が直交行列となるように
Next: 12 直交変換 Up: 2 線形写像 Previous: 10 正則変換 Contents
Kondo Koichi

Created at 2004/12/13