Next: 14 表現行列と基底の変換行列 Up: 2 線形写像 Previous: 12 直交変換 Contents
13 回転移動
例 2.61 (
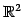 の回転)
直交変換
の回転)
直交変換
を考える. この直交変換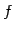 は
は
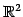 内の
点を原点を中心に反時計回りに角
内の
点を原点を中心に反時計回りに角 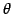 回転移転を表す.
直交行列
回転移転を表す.
直交行列 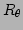 は
は
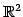 の回転行列という.
の回転行列という.
とおく.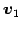 ,
, 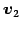 はそれぞれ
はそれぞれ
 ,
, 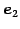 を原点を中心に
を原点を中心に 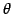 回転させた
ベクトルである.
次に,任意のベクトル
回転させた
ベクトルである.
次に,任意のベクトル
を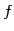 で写すと
で写すと
と表される.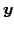 は基底
は基底
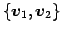 における
座標
における
座標 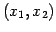 の点である.
元の点
の点である.
元の点 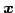 は標準基底
は標準基底
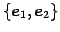 における
座標
における
座標 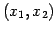 の点であるので,
の点であるので,
 は原点を中心に
は原点を中心に  回転した点となる.
回転した点となる.
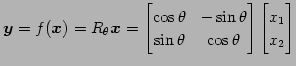 |
を考える. この直交変換
標準基底 ![]() ,
, ![]() を
を ![]() で写したベクトルを
で写したベクトルを
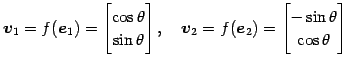 |
とおく.
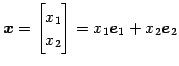 |
を
と表される.
問 2.62 (直交行列と回転行列)
 をみたす
をみたす  型の実行列は回転行列のみである.
これを示せ.
型の実行列は回転行列のみである.
これを示せ.
例 2.63 (
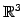 の回転)
直交変換
の回転)
直交変換
を考える. この写像は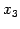 軸を中心に
軸を中心に 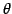 回転を表す.
回転を表す.
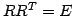 より
より 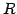 は直交行列である.
は直交行列である.
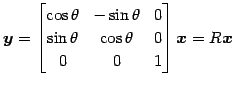 |
を考える. この写像は
例 2.64 (
 の回転)
の回転)
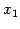 軸まわりの回転:
軸まわりの回転:
 軸まわりの回転:
軸まわりの回転:
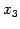 軸まわりの回転:
軸まわりの回転:
 ,
, 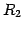 ,
, 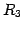 は直交行列である.
は直交行列である.
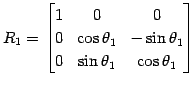 |
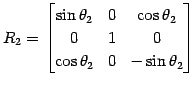 |
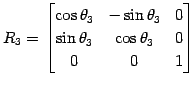 |
![]() 軸まわりに回転し,その後
軸まわりに回転し,その後 ![]() 軸まわりに回転させるとき,
表現行列は
軸まわりに回転させるとき,
表現行列は ![]() である.これもまた直交行列である.
同様に
である.これもまた直交行列である.
同様に ![]() ,
, ![]() ,
, ![]() もまた回転を表す.
ただし,
もまた回転を表す.
ただし,
![]() であることに注意すること.
回転する順番が違えば異なる回転を表すからである.
であることに注意すること.
回転する順番が違えば異なる回転を表すからである.
Next: 14 表現行列と基底の変換行列 Up: 2 線形写像 Previous: 12 直交変換 Contents
Kondo Koichi

Created at 2004/12/13