Next: 11 直交行列 Up: 2 線形写像 Previous: 9 線形写像の合成写像 Contents
10 正則変換
定義 2.41 (正則変換)
線形変換 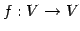 が上への 1 対 1 写像であるとき,
が上への 1 対 1 写像であるとき,
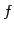 を正則変換(regular mappping) という.
を正則変換(regular mappping) という.
注意 2.42 (逆変換)
上への 1 対 1 写像であれば逆変換 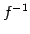 が存在する.
正則変換は逆変換が存在する線形変換である,と読み替えてもよい.
が存在する.
正則変換は逆変換が存在する線形変換である,と読み替えてもよい.
定理 2.43 (正則変換と正則行列)
線形写像 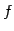 が正則変換であることと,
が正則変換であることと,
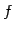 の表現行列が正則行列であることとは必用十分な条件である.
の表現行列が正則行列であることとは必用十分な条件である.
と表される.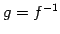 のとき
のとき
が成り立つ.よって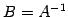 である.
である.
(証明) 合成写像と表現行列は
と表される.
が成り立つ.よって
注意 2.44 (逆変換と逆行列)
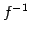 が存在するとき表現行列
が存在するとき表現行列 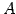 の逆行列
の逆行列 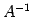 も存在する.
も存在する.
例 2.45 (正則変換の具体例)
線形写像
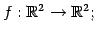
の表現行列とその行列式は
である.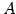 は正則行列であるから,
は正則行列であるから,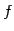 は正則変換である.
は正則変換である.
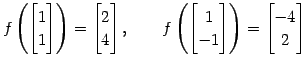 |
の表現行列とその行列式は
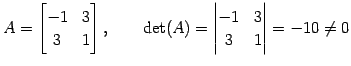 |
である.
例 2.46 (正則変換ではない具体例)
射影変換
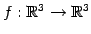 ;
;
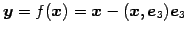 の
表現行列とその行列式は
の
表現行列とその行列式は
である. よって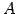 は正則でないので
は正則でないので 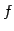 もまた正則ではない.
もまた正則ではない.
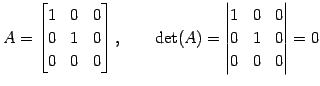 |
である. よって
例えば点
![]() と点
と点
![]() を
射影変換
を
射影変換 ![]() で写すとどちらも点
で写すとどちらも点
![]() に写される.
他にも点
に写される.
他にも点
![]() を通り軸
を通り軸 ![]() に平行な直線上の点は全て
に平行な直線上の点は全て
![]() により点
により点
![]() に写される.
逆変換
に写される.
逆変換 ![]() を考えるとき点
を考えるとき点
![]() から戻され点は
直線上に無限に存在することになる.
よって
から戻され点は
直線上に無限に存在することになる.
よって ![]() は 1 対 1 写像ではない.
また,
は 1 対 1 写像ではない.
また,
![]() の任意の点は
の任意の点は ![]() により
全て
により
全て
![]() 平面上に写される.
平面上に写される.
![]() 平面は
平面は
![]() の部分空間であるので,
の部分空間であるので,
![]() は上への写像でもない.
は上への写像でもない.
Next: 11 直交行列 Up: 2 線形写像 Previous: 9 線形写像の合成写像 Contents
Kondo Koichi

Created at 2004/12/13