Next: 10 正則変換 Up: 2 線形写像 Previous: 8 線形変換 Contents
9 線形写像の合成写像
定義 2.37 (合成写像)
線形写像 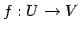 ;
;
 と
と
 ;
;
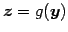 より定まる写像
より定まる写像
を と
と  の合成写像(composite)といい,
の合成写像(composite)といい,
と表記する.
を
と表記する.
定理 2.38 (線形写像の合成写像)
線形写像の合成写像もまた線形写像となる.
定理 2.39 (合成写像の表現行列)
線形写像  ,
,  の表現行列をそれぞれ
の表現行列をそれぞれ 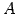 ,
,  とする.
このとき,
合成写像
とする.
このとき,
合成写像
 の表現行列は
の表現行列は 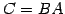 となる.
となる.
例 2.40 (合成写像の表現行列の具体例)
を考える.このとき
である. 表現行列は
となる.
を考える.このとき
である. 表現行列は
となる.
Kondo Koichi

Created at 2004/12/13