Next: 26 直交補空間 Up: 1 ベクトル空間 Previous: 24 ベクトル空間の和 Contents
25 直和分解
定義 1.113 (直和分解)
ベクトル空間 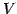 とその部分空間
とその部分空間 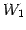 ,
, 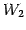 が
が
をみたすとき,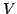 を
を 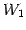 と
と 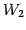 に直和分解するという.
に直和分解するという.
をみたすとき,
例 1.114 (直和分解の具体例)
ベクトル
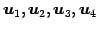 を 1 次独立とする.
このとき
を 1 次独立とする.
このとき
が成り立つ.
が成り立つ.
Kondo Koichi

Created at 2004/12/13