Next: 25 直和分解 Up: 1 ベクトル空間 Previous: 23 連立 1 次方程式の図形的イメージ Contents
24 ベクトル空間の和
定義 1.105 (ベクトル空間の和)
ベクトル空間  ,
, 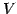 に対して
に対して
をベクトル空間の和という. 特に,
のとき
と表記し,直和という.
をベクトル空間の和という. 特に,
のとき
と表記し,直和という.
注意 1.106 (直和)
ベクトル空間 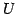 ,
, 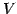 ,
, 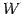 が
が
であるとする. このとき,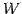 のあるベクトル
のあるベクトル 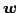 に対して,
に対して,
をみたす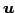 ,
, 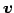 はただ一つ定まる.
はただ一つ定まる.
であるとする. このとき,
をみたす
定理 1.107 (ベクトル空間の和の次元)
ベクトル空間 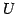 ,
, 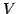 ,
, 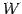 が
が
をみたすとき,
である.
をみたすとき,
である.
をみたすとき,
である.
をみたすとき,
である.
定理 1.108 (部分空間の共通部分)
ベクトル
が 1 次独立であるとき, これらのベクトルで生成される空間
の共通部分は
となる.
と表される. ここで,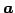 ,
, 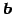 ともに
ともに
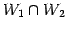 のベクトルとする.
すなわち,
のベクトルとする.
すなわち,
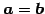 とする.
このとき,
とする.
このとき,
と 1 次関係を得る. ベクトル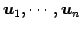 ,
,
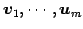 は 1 次独立なので
係数は
は 1 次独立なので
係数は
と自明なものに限る. よって共通のベクトルは零ベクトル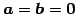 に限る.
に限る.
が 1 次独立であるとき, これらのベクトルで生成される空間
の共通部分は
となる.
(証明)
![]() と
と ![]() の任意のベクトルは
の任意のベクトルは
と表される. ここで,
と 1 次関係を得る. ベクトル
と自明なものに限る. よって共通のベクトルは零ベクトル
定理 1.109 (部分空間の共通部分)
ベクトル
が 1 次独立であるとき, これらのベクトルで生成される空間
の共通部分は
となる.
が 1 次独立であるとき, これらのベクトルで生成される空間
の共通部分は
となる.
例 1.110 (ベクトル空間の和の具体例)
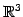 の部分空間
の部分空間 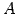 ,
,  の和を考える.
の和を考える.
が成り立つ. 直線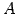 が平面
が平面 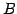 上にあるとき,
上にあるとき,
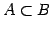 であるので,
であるので,
が成り立つ.
が成り立つ. であるときは,
であるときは,
が成り立つ.
(1)
原点を通る直線 ![]() と平面
と平面 ![]() を考える.
直線
を考える.
直線 ![]() が原点以外で平面
が原点以外で平面 ![]() と交わらないとき,
と交わらないとき,
![]() であり,
であり,
が成り立つ. 直線
が成り立つ.
(2)
原点を通る平面 ![]() と平面
と平面 ![]() を考える.
を考える.
![]() であるとき
であるとき
![]() と
と ![]() とが交わる点の集合は直線
とが交わる点の集合は直線 ![]() となる.
となる.
![]() である.
このとき,
である.
このとき,
が成り立つ.
が成り立つ.
例 1.111 (ベクトル空間の和の具体例)
 の部分空間
の部分空間 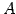 ,
,  ,
, 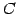 の和を考える.
の和を考える.
が成り立つ.
が成り立つ.
(1) 原点を通る直線 ![]() ,
, ![]() を考える.
を考える.
![]() であるとき,
であるとき,
![]() であるから,
であるから,
が成り立つ.
(2) 原点を通る直線 ![]() と平面
と平面 ![]() を考える.
を考える.
![]() ,
,
![]() であり,
であり,
![]() であるから,
であるから,
が成り立つ.
例 1.112 (ベクトル空間の和の具体例)
ベクトル
 を
1 次独立とする.
これらで生成される部分空間
を
1 次独立とする.
これらで生成される部分空間
を考える. これらの和は
と表される.
を考える. これらの和は
と表される.
Next: 25 直和分解 Up: 1 ベクトル空間 Previous: 23 連立 1 次方程式の図形的イメージ Contents
Kondo Koichi

Created at 2004/12/13