Next: 27 基底の変換 Up: 1 ベクトル空間 Previous: 25 直和分解 Contents
26 直交補空間
定義 1.115 (ベクトルと部分空間の直交)
ベクトル
 と
部分空間
と
部分空間
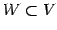 に含まれるすべてのベクトル
に含まれるすべてのベクトル  とが
直交するとき,すなわち
とが
直交するとき,すなわち
が成り立つとき,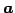 と
と  とは直交するといい,
とは直交するといい,
と表記する.
が成り立つとき,
と表記する.
例 1.116 (ベクトルと部分空間とが直交する具体例)
 の部分空間
の部分空間
とベクトル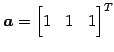 と
は直交
と
は直交
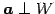 する.
なぜなら,
する.
なぜなら, は方程式
は方程式
 の
解空間として表されるからである.
この例では
の
解空間として表されるからである.
この例では 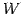 は平面であり
は平面であり 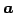 は法線ベクトルである.
は法線ベクトルである.
とベクトル
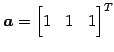 と
は直交
と
は直交
定義 1.117 (直交補空間)
ベクトル空間 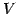 とその部分空間
とその部分空間  に対して,
部分空間
に対して,
部分空間
を における
における 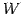 の直交補空間という.
の直交補空間という.
を
定理 1.118 (直交補空間による直和分解)
ベクトル空間 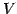 における部分空間
における部分空間 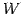 の直交補空間
の直交補空間 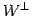 は
は
となる.次元は
の関係が成り立つ.
となる.次元は
の関係が成り立つ.
定理 1.119 (直交補空間の次元)
部分空間
の次元は
である.ただし,
とおく. の直交補空間
の直交補空間  は
方程式
は
方程式
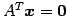 の解空間であり,
の解空間であり,
となり,次元は
である.
の次元は
である.ただし,
とおく.
となり,次元は
である.
例 1.120 (直交補空間の具体例)
部分空間
に対する直交補空間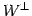 を求める.
を求める.
 の任意のベクトルを
の任意のベクトルを 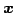 とする.
とする.
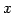 は
は 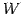 の任意のベクトル
の任意のベクトル
 と
直交するので
と
直交するので
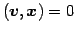 が成り立つ.
こりより,
が成り立つ.
こりより,
と表される. すべての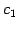 ,
, 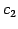 について成り立つためには
について成り立つためには
をみたさなければならない. この連立方程式を書き直すと
であり,
となる. これを解く. 係数行列を簡約化すると
となるので,解は
となる. よって,直交補空間は
と得られる.
が成り立つ. また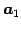 ,
,  ,
,  は
は
 の
基底となることに注意する.
つまり
の
基底となることに注意する.
つまり
である.
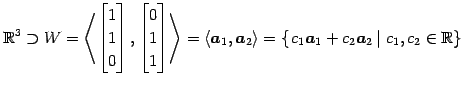 |
に対する直交補空間
と表される. すべての
をみたさなければならない. この連立方程式を書き直すと
であり,
 |
となる. これを解く. 係数行列を簡約化すると
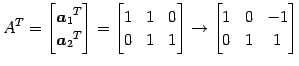 |
となるので,解は
 |
となる. よって,直交補空間は
 |
と得られる.
![]() の基底
の基底
![]() と
と ![]() の基底
の基底 ![]() とは
1 次独立である.
よって
とは
1 次独立である.
よって
![]() であるので,
であるので,
が成り立つ. また
である.
例 1.121 (直交補空間の具体例)
ベクトル
 を
正規直交基底とする.
このとき
を
正規直交基底とする.
このとき
が成り立つ. ここで
とおくと,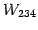 は
は
 における
における  の直交補空間となる.
なぜなら任意のベクトル
の直交補空間となる.
なぜなら任意のベクトル
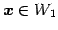 ,
,
 に対して
に対して
が成り立ち, と
と  は直交するからである.
よって
は直交するからである.
よって
であり,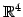 は
は 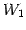 とその直交補空間
とその直交補空間 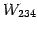 に
よって直和分解される.
同様に
に
よって直和分解される.
同様に
と部分空間とのその直交補空間とで直和分解される. ただし,
とおく.
が成り立つ. ここで
とおくと,
が成り立ち,
であり,
と部分空間とのその直交補空間とで直和分解される. ただし,
とおく.
例 1.122 (直交補空間の具体例)
正規直交基底
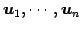 で
生成されるベクトル空間
で
生成されるベクトル空間
を考える.このとき は直和分解されて
は直和分解されて
と表される. は
は  における
における  の直交補空間である.
さらに
の直交補空間である.
さらに 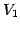 を直和分解して
を直和分解して
と表される. は
は 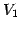 における
における 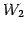 の直交補空間である.
同様に繰り返して直交補空間で直和分解が可能である:
の直交補空間である.
同様に繰り返して直交補空間で直和分解が可能である:
を考える.このとき
と表される.
と表される.
Next: 27 基底の変換 Up: 1 ベクトル空間 Previous: 25 直和分解 Contents
Kondo Koichi

Created at 2004/12/13