Next: 22 解空間 Up: 1 ベクトル空間 Previous: 20 正規直交基底 Contents
21 グラム・シュミットの直交化法
定義 1.95 (正規直交化)
ベクトル空間
の基底を取り替えて
とする. このとき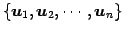 が
正規基底となるとき,
この操作を正規化(normalize)という.
直交基底となるとき,直交化(orthogonalize)という.
正規直交基底となるとき,正規直交化(orthonormalize)という.
が
正規基底となるとき,
この操作を正規化(normalize)という.
直交基底となるとき,直交化(orthogonalize)という.
正規直交基底となるとき,正規直交化(orthonormalize)という.
の基底を取り替えて
とする. このとき
定理 1.96 (正規化)
ベクトル空間 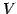 の
基底
の
基底
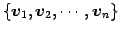 に対して
次の式で定まる
に対して
次の式で定まる
 は
正規基底となる:
は
正規基底となる:
定理 1.97 (グラム・シュミットの直交化法)
ベクトル空間 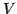 の基底
の基底
 に
対して次の式で定まる
に
対して次の式で定まる
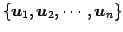 は
は
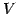 の正規直交基底となる.
この手法をグラム・シュミットの直交化法という.
の正規直交基底となる.
この手法をグラム・シュミットの直交化法という.
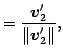 |
||||
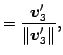 |
||||
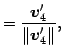 |
||||
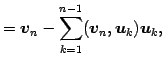 |
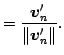 |
(証明)
例 1.98 (グラム・シュミットの直交化法の具体例)
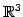 の基底
の基底
を正規直交化する. グラム・シュミットのの直交化法より,
となる. 以上よりベクトル
は
をみたし,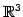 の正規直交基底となる.
の正規直交基底となる.
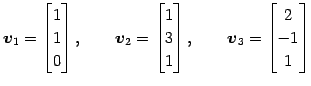 |
を正規直交化する. グラム・シュミットのの直交化法より,
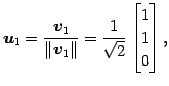 |
||
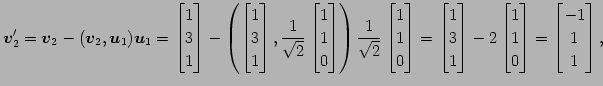 |
||
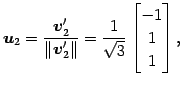 |
||
 |
||
 |
||
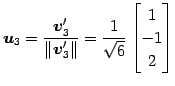 |
となる. 以上よりベクトル
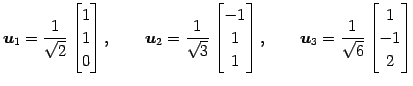 |
は
をみたし,
Next: 22 解空間 Up: 1 ベクトル空間 Previous: 20 正規直交基底 Contents
Kondo Koichi

Created at 2004/12/13