Next: 21 グラム・シュミットの直交化法 Up: 1 ベクトル空間 Previous: 19 次元 Contents
20 正規直交基底
定義 1.90 (正規直交基底)
ベクトル空間の基底
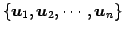 に
対して次の名称を定義する:
に
対して次の名称を定義する:
- 正規基底(normal basis):
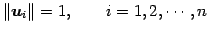
- 直交基底(orthogonal basis):
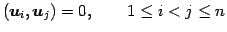
- 正規直交基底(orthonormal basis):

例 1.91 (基本ベクトルの正規直交性)
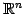 の
標準基底
の
標準基底
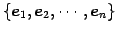 は
正規直交基底である.
は
正規直交基底である.
(証明)
例 1.92 (基本ベクトルの正規直交性)
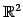 の基底
の基底
は
をみたすので正規直交基底である.
 |
は
をみたすので正規直交基底である.
例 1.93 (正規直交系の具体例)
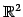 の基底
の基底
は
をみたすので正規直交基底である.
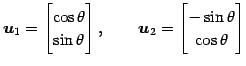 |
は
をみたすので正規直交基底である.
定理 1.94 (正規直交基底における 1 次結合)
正規直交基底
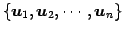 に
より定まるベクトル
に
より定まるベクトル
の係数は
により定まる.
の両辺との内積をとると
を得る.
の係数は
により定まる.
(証明)
ベクトル ![]() と
と
の両辺との内積をとると
を得る.
Next: 21 グラム・シュミットの直交化法 Up: 1 ベクトル空間 Previous: 19 次元 Contents
Kondo Koichi

Created at 2004/12/13