Next: 23 連立 1 次方程式の図形的イメージ Up: 1 ベクトル空間 Previous: 21 グラム・シュミットの直交化法 Contents
22 解空間
定義 1.99 (解空間)
同次系
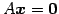 の解の集合
の解の集合
を解空間(solution space)という.
を解空間(solution space)という.
定理 1.100 (解空間と部分空間)
解空間 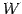 は
は
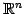 の部分空間である.
の部分空間である.
をみたすとする. このとき,
となるので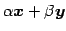 もまた解である.
よって
もまた解である.
よって
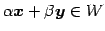 となり,
となり,
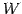 は部分空間である.
は部分空間である.
(証明)
![]() とする.
すなわち,
とする.
すなわち,![]() ,
, ![]() は方程式
は方程式
![]() の解であり,
の解であり,
をみたすとする. このとき,
となるので
注意 1.101 (非同次系の解空間)
非同次系
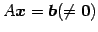 の解空間
の解空間 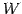 は
は
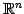 の部分空間ではない.
なぜなら,
の部分空間ではない.
なぜなら,
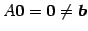 より
非同次系は原点
より
非同次系は原点 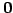 を解にもたない.
よって
を解にもたない.
よって 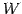 は
は 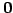 を含まず,部分空間とはならない.
つまり,
を含まず,部分空間とはならない.
つまり,
である.
である.
定理 1.102 (解空間の次元)
同次系の解空間 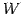 の次元は一般解の任意定数の個数と等しく,
の次元は一般解の任意定数の個数と等しく,
で与えられる.
で与えられる.
定義 1.103 (一般解)
解空間 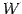 の基底
の基底
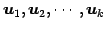 を
方程式
を
方程式
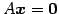 の基本解という.
このとき
の基本解という.
このとき 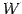 の任意のベクトルは
基本解の線形結合で
の任意のベクトルは
基本解の線形結合で
と表される. これを方程式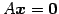 の一般解という.
の一般解という.
と表される. これを方程式
例 1.104 (解空間の具体例)
解空間
を考える. 方程式を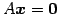 とおく.
とおく.
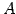 を簡約化して
を簡約化して
となる. これより,方程式は
と書き換わる.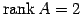 より任意定数の個数は
より任意定数の個数は
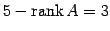 となり,
任意定数を
となり,
任意定数を
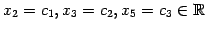 とおく.
よって一般解は
とおく.
よって一般解は
と得られる. ここで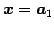 ,
,
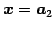 ,
,
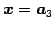 は基本解である.
解空間は
は基本解である.
解空間は
となる.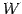 の基底を求める.
の基底を求める.
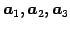 が 1 次独立であるか調べる.
1 次関係
が 1 次独立であるか調べる.
1 次関係
より
となる. よって条件をみたすのは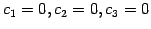 のときのみである.
のときのみである.
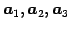 は 1 次独立である.
は 1 次独立である.
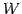 の基底は
の基底は
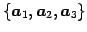 となる.
以上より
となる.
以上より
を得る. これは解の任意定数の個数に等しい.
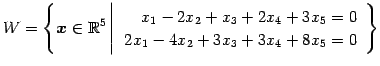 |
を考える. 方程式を
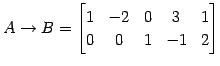 |
となる. これより,方程式は
と書き換わる.
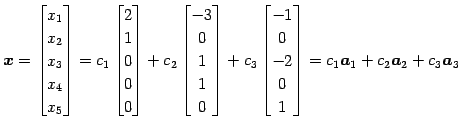 |
と得られる. ここで
となる.
より
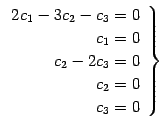 |
となる. よって条件をみたすのは
を得る. これは解の任意定数の個数に等しい.
Next: 23 連立 1 次方程式の図形的イメージ Up: 1 ベクトル空間 Previous: 21 グラム・シュミットの直交化法 Contents
Kondo Koichi

Created at 2004/12/13