Next: 13 1 次独立と 1 Up: 1 ベクトル空間 Previous: 11 ベクトルの直交 Contents
12 基本ベクトル
定義 1.51 (基本ベクトル)
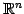 のベクトル
のベクトル
を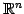 の
基本ベクトル(elemental vector)という.
の
基本ベクトル(elemental vector)という.
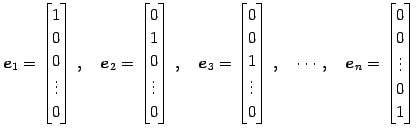 |
(37) |
を
定理 1.52 (基本ベクトルと任意のベクトル)
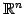 の任意のベクトル
の任意のベクトル
は
と表される.
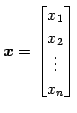 |
は
と表される.
Kondo Koichi

Created at 2004/12/13