Next: 12 基本ベクトル Up: 1 ベクトル空間 Previous: 10 ベクトルのなす角 Contents
11 ベクトルの直交
定義 1.48 (ベクトルの直交)
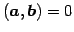 のとき
のとき 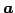 と
と 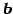 は
直交する(orthogonal)という.
このとき
は
直交する(orthogonal)という.
このとき
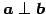 と表記する.
と表記する.
例 1.49 (ベクトルの直交の具体例)
を考える.このとき
が成り立つ.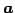 と
と 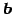 は互いに直交する.
は互いに直交する.
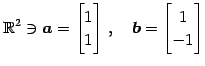 |
(33) |
を考える.このとき
| (34) |
が成り立つ.
例 1.50 (ベクトルの直交の具体例)
を考える.このとき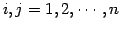 に対して
に対して
が成り立つ. よって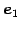 ,
,
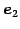 ,
, 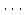 ,
,
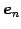 は
互いに直交する.
は
互いに直交する.
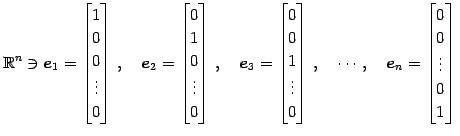 |
(35) |
を考える.このとき
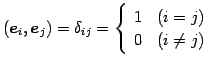 |
(36) |
が成り立つ. よって
Kondo Koichi

Created at 2004/12/13