Next: 14 1 次結合の記法 Up: 1 ベクトル空間 Previous: 12 基本ベクトル Contents
13 1 次独立と 1 次従属
定義 1.53 (1 次結合,1 次従属)
ベクトル
 に対して,
ベクトル
に対して,
ベクトル
を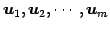 の
1 次結合または線形結合(linear combination)
という.
またこのとき,
ベクトル
の
1 次結合または線形結合(linear combination)
という.
またこのとき,
ベクトル 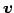 は
は
 に
1 次従属または線形従属(linearly dependent)
という.
に
1 次従属または線形従属(linearly dependent)
という.
を
定義 1.54 (1 次関係,1 次独立,1 次従属)
ベクトル
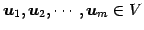 に対して,
条件式
に対して,
条件式
を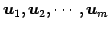 の
1 次関係という.
の
1 次関係という.
を
1 次関係をみたす係数が
![]() ときのみであるとき,
ときのみであるとき,
![]() は
1 次独立または線形独立(linearly independent)
という.
は
1 次独立または線形独立(linearly independent)
という.
![]() が
1 次独立ではないしき,
1 次従属または線形従属という.
が
1 次独立ではないしき,
1 次従属または線形従属という.
注意 1.55 (自明な 1 次関係)
1 次関係
において
とおくと,明らかに 1 次関係は成立する. このとき自明な 1 次関係という. 自明な 1 次関係のときベクトルは 1 次独立である. また, 自明な 1 次関係ではないとき非自明な 1 次関係という. 非自明な 1 次関係のときベクトルは 1 次従属である. 非自明な場合は例えば
等々がある.
において
とおくと,明らかに 1 次関係は成立する. このとき自明な 1 次関係という. 自明な 1 次関係のときベクトルは 1 次独立である. また, 自明な 1 次関係ではないとき非自明な 1 次関係という. 非自明な 1 次関係のときベクトルは 1 次従属である. 非自明な場合は例えば
等々がある.
例 1.56 (ベクトルの 1 次独立,1 次従属の具体例)
ベクトル
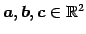 を考える.
を考える.
となので,非自明な 1 次関係である. よって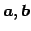 は 1 次従属である.
は 1 次従属である.
は自明なもののみである. もし非自明であれば同時には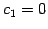 ,
,  とはならないので,
とはならないので,
 とおく.
このとき
とおく.
このとき
と表される.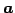 と
と 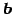 は同じ向きとなる.
これは与えられた条件と矛盾する.
よって 1 次関係は自明なものに限る.
は同じ向きとなる.
これは与えられた条件と矛盾する.
よって 1 次関係は自明なものに限る.
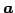 ,
, 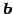 は 1 次独立である.
は 1 次独立である.
となる.非自明な 1 次関係であるから, は 1 次従属である.
は 1 次従属である.
(i) ![]() ,
, ![]() が同じ向きのときを考える.
向きが同じなので
が同じ向きのときを考える.
向きが同じなので
![]() と書ける.また,
と書ける.また,
となので,非自明な 1 次関係である. よって
(ii) ![]() ,
, ![]() の向きが異なるときを考える.
このとき 1 次関係
の向きが異なるときを考える.
このとき 1 次関係
は自明なもののみである. もし非自明であれば同時には
と表される.
(iii)
![]() となるときを考える.
条件を書き換えると
となるときを考える.
条件を書き換えると
となる.非自明な 1 次関係であるから,
例 1.57 (基本ベクトルの 1 次独立性)
基本ベクトル
 は
1 次独立である.
なぜなら, 1 次関係は
は
1 次独立である.
なぜなら, 1 次関係は
となるので,係数は自明
なものに限るからである.
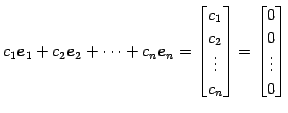 |
となるので,係数は自明
なものに限るからである.
例 1.58 (1 次独立の具体例)
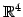 のベクトル
のベクトル
は 1 次独立であるか考える. これらの 1 次関係
をみたす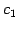 ,
, 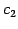 ,
,  を定める.
1 次関係を変形して
を定める.
1 次関係を変形して
であり,
となり,
と表される. 行列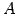 を簡約化すると
を簡約化すると
である.よって
を得る. 係数は自明なもの
に限るので,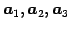 は 1 次独立である.
は 1 次独立である.
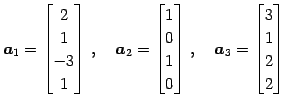 |
は 1 次独立であるか考える. これらの 1 次関係
をみたす
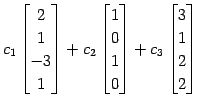 |
であり,
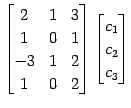 |
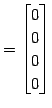 |
となり,
と表される. 行列
 |
である.よって
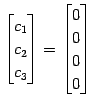 |
を得る. 係数は自明なもの
に限るので,
例 1.59 (1 次従属の具体例)
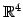 のベクトル
のベクトル
は 1 次独立であるか考える. 1 次関係より,
となる. 簡約化すると
であるから,
を得る. 1 次関係は
となる.非自明な 1 次関係であるから, は 1 次従属である.
は 1 次従属である.
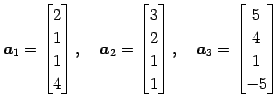 |
は 1 次独立であるか考える. 1 次関係より,
 |
||
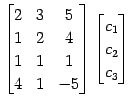 |
||
となる. 簡約化すると
 |
であるから,
 |
を得る. 1 次関係は
となる.非自明な 1 次関係であるから,
まとめ 1.60 (1 次独立性の判定)
ベクトル
 の 1 次独立性を考える.
これらのベクトルを列ベクトルにもつ行列を
の 1 次独立性を考える.
これらのベクトルを列ベクトルにもつ行列を
とおく.このとき に関する方程式
に関する方程式
の解の任意定数の個数は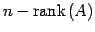 であるから,次の関係が成り立つ:
であるから,次の関係が成り立つ:
とおく.このとき
の解の任意定数の個数は
定理 1.61 (1 次独立の性質)
定理 1.62 (1 次独立の性質)
定理 1.63 (1 次独立の性質)
Next: 14 1 次結合の記法 Up: 1 ベクトル空間 Previous: 12 基本ベクトル Contents
Kondo Koichi

Created at 2004/12/13