Next: 11 ベクトルの直交 Up: 1 ベクトル空間 Previous: 9 単位ベクトル Contents
10 ベクトルのなす角
定義 1.45 (ベクトルの成す角)
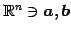 に対して
に対して
により得られる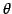 を
ベクトル
を
ベクトル 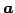 と
と 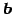 との成す角(angular)という.
との成す角(angular)という.
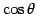 を方向余弦(direction cosine)という.
を方向余弦(direction cosine)という.
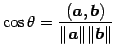 |
(28) |
により得られる
注意 1.46 (内積とノルムの比)
シュバルツの不等式より
となることに注意する.
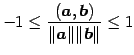 |
(29) |
となることに注意する.
例 1.47 (成す角の具体例)
を考える.このとき方向余弦は
となるので, 成す角は
である.
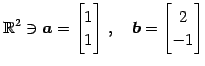 |
(30) |
を考える.このとき方向余弦は
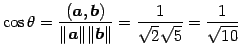 |
(31) |
となるので, 成す角は
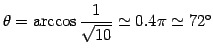 |
(32) |
である.
Kondo Koichi

Created at 2004/12/13