Next: 9 単位ベクトル Up: 1 ベクトル空間 Previous: 7 内積 Contents
8 ノルム
定義 1.37 (ノルム)
ベクトル
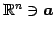 または
または
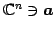 に対して
に対して
をベクトルのノルム(norm)または 長さ(length)という.
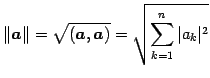 |
(17) |
をベクトルのノルム(norm)または 長さ(length)という.
例 1.38 (ノルムの具体例)
のノルムはそれぞれ
である.
のノルムはそれぞれ
である.
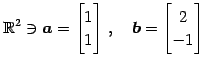 |
(18) |
のノルムはそれぞれ
| (19) | ||
| (20) |
である.
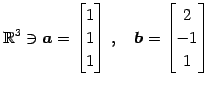 |
(21) |
のノルムはそれぞれ
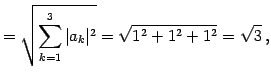 |
(22) | |
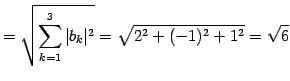 |
(23) |
である.
定理 1.39 (ノルムの性質)
シュバルツの不等式(Schwartz' inequality):
三角不等式:
| (24) |
三角不等式:
| (25) |
定義 1.40 (ノルム)
ノルムはシュバルツの不等式と三角不等式をみたすものであればよい.
次に定義される式もノルムとなる.
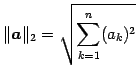 |
||
![$\displaystyle \Vert\vec{a}\Vert _{3}=\sqrt[3]{\sum_{k=1}^{n}(a_{k})^3}$](img332.png) |
||
![$\displaystyle \Vert\vec{a}\Vert _{p}=\sqrt[p]{\sum_{k=1}^{n}(a_{k})^p}$](img334.png) |
||
Next: 9 単位ベクトル Up: 1 ベクトル空間 Previous: 7 内積 Contents
Kondo Koichi

Created at 2004/12/13