Next: 8 ノルム Up: 1 ベクトル空間 Previous: 6 ベクトル空間 Contents
7 内積
定義 1.29 (内積)
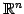 の 2 つのベクトル
の 2 つのベクトル
に対して
なる二項演算を内積(inner product)という. また,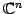 のベクトル
のベクトル
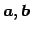 に対しては
に対しては
と定義する.
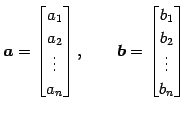 |
に対して
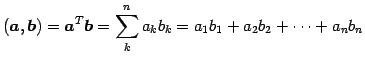 |
(11) |
なる二項演算を内積(inner product)という. また,
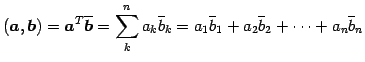 |
(12) |
と定義する.
例 1.30 (内積の具体例)
ベクトル
の内積は
である.また
の内積は
である.
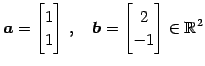 |
(13) |
の内積は
| (14) |
である.また
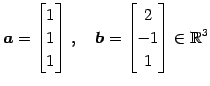 |
(15) |
の内積は
| (16) |
である.
定理 1.31 (内積の性質)
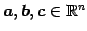 と
と
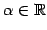 に対して
に対して
- (i)
- (内積の交換則)
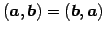 .
.
- (ii)
- (内積の分配則)
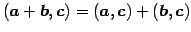 .
.
- (iii)
- (内積のスカラー倍の結合則)
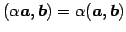 ,
,
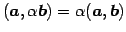 .
.
- (iv)
-
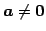 のとき
のとき
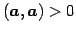
問 1.32 (内積の性質)
これを示せ.
定理 1.33 (内積の性質)
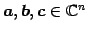 と
と
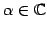 に対して
に対して
- (i)
- (内積の交換則)
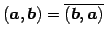 .
.
- (ii)
- (内積の分配則)
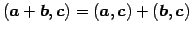 .
.
- (iii)
- (内積のスカラー倍の結合則)
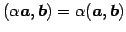 ,
,
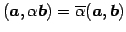 .
.
- (iv)
-
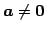 のとき
のとき
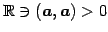
問 1.34 (内積の性質)
これを示せ.
定義 1.35 (内積空間)
内積が定義されたベクトル空間を
内積空間(inner product space)という.
注意 1.36 (行列の積と内積)
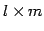 型行列
型行列 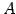 を行ベクトルに分割し,
を行ベクトルに分割し,
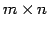 型行列
型行列 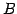 を列ベクトルに分割し
を列ベクトルに分割し
とおく. ただし,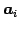 ,
, 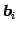 は
は 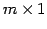 型の列ベクトルである.
このとき積は
型の列ベクトルである.
このとき積は
と表される.
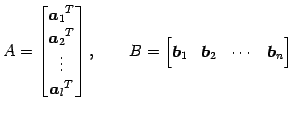 |
とおく. ただし,
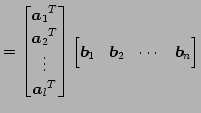 |
||
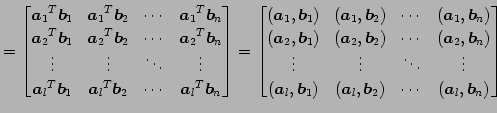 |
と表される.
Next: 8 ノルム Up: 1 ベクトル空間 Previous: 6 ベクトル空間 Contents
Kondo Koichi

Created at 2004/12/13