Next: 6 行列式の列に関する性質 Up: 4 行列式 Previous: 4 行列式の定義 Contents
5 行列式の行に関する性質
定理 4.42 (行列式の行に関する性質)
行列式は次の性質もつ.
- (1)
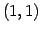 成分を除いて
成分を除いて 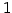 列目が全て 0 の場合は
行列式のサイズが一つ下がる.
列目が全て 0 の場合は
行列式のサイズが一つ下がる.
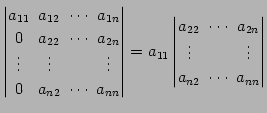
(650)
- (2)
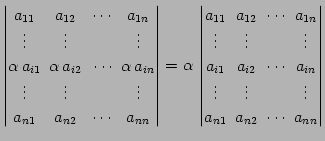
- 第
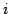 行目の要素全てが共通因子
行目の要素全てが共通因子 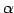 をもつとき,
をもつとき,
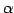 は行列式の外へ.
は行列式の外へ.
(651)
- (3)
- 第
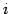 行が二つのベクトルの和で表されるとき,
行列式の和に分解される.
行が二つのベクトルの和で表されるとき,
行列式の和に分解される.

(652)
- (4)
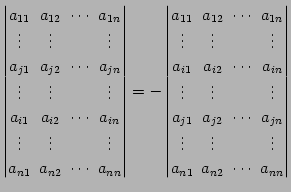
- 第
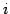 行と第
行と第 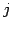 行を入れ替えると
行列式の符合が反転する.
行を入れ替えると
行列式の符合が反転する.
(653)
- (5)
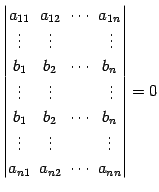
- 同じ行があるときは行列式は 0 となる.
(654)
- (6)
- 第
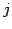 行を
行を 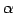 倍して
第
倍して
第 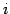 行に加えても行列式は等しい.
行に加えても行列式は等しい.

(655)
問 4.43 (行列式の行に関する性質)
これを示せ.
Kondo Koichi

Created at 2004/11/26