Next: 5 行列式の行に関する性質 Up: 4 行列式 Previous: 3 多項式の文字の置換 Contents
4 行列式の定義
定義 4.38 (行列式)
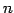 次正方行列
次正方行列
![$ A=[a_{ij}]_{m\times n}$](img2039.png) に対して
に対して
を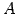 の行列式(determinant)という.
の行列式(determinant)という.
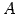 の行列式はまた
の行列式はまた
と書き表す.
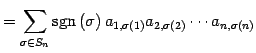 |
(636) |
を
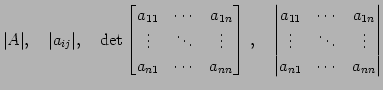 |
(637) |
と書き表す.
例 4.39 (行列式の具体例)
 のとき,
のとき,
より,行列式は
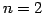 のとき,
のとき,
より, 行列式は
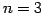 のとき,
のとき,
より,行列式は
| (638) |
より,行列式は
 |
(639) |
| (640) |
より, 行列式は
 |
(641) | |
| (642) | ||
| (643) |
| (644) |
より,行列式は
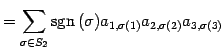 |
(645) | |
| (646) |
問 4.40 (行列式の具体例)
 次の行列式を定義に従い書き下せ.
次の行列式を定義に従い書き下せ.
注意 4.41 (サルスの方法)
 次の行列式まではサルスの方法により
符合が簡単に定まる.
右斜め下向きの組合わせでは正をとり,
左斜め下向きの組合わせでは負となる.
次の行列式まではサルスの方法により
符合が簡単に定まる.
右斜め下向きの組合わせでは正をとり,
左斜め下向きの組合わせでは負となる.
 次以上の行列式ではこのルールは適用できない.
次以上の行列式ではこのルールは適用できない.
| (647) | ||
 |
(648) | |
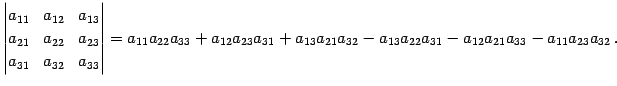 |
(649) |
Next: 5 行列式の行に関する性質 Up: 4 行列式 Previous: 3 多項式の文字の置換 Contents
Kondo Koichi

Created at 2004/11/26