Next: 23 点の平面への射影 Up: 1 ベクトルと図形 Previous: 21 平面の方程式 Contents
22 平面と直線の交点
注意 1.106 (平面と直線の交点)
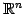 空間内の平面
空間内の平面
と直線
との交点を考える. これを平面の方程式に代入すると
であるから,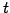 についてまとめると
についてまとめると
を得る. よって直線の方程式に代入すると
となる. 平面と直線の交点の位置ベクトルは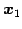 である.
である.
| (171) |
と直線
| (172) |
との交点を考える. これを平面の方程式に代入すると
| (173) |
であるから,
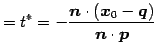 |
(174) |
を得る. よって直線の方程式に代入すると
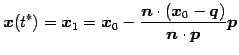 |
(175) |
となる. 平面と直線の交点の位置ベクトルは
例 1.107 (平面と直線の交点の具体例)
平面
と直線
との交点を考える. 直線の方程式のパラメータ表示は
である.これを平面の方程式に代入すると
より
を得る. 直線の方程式のパラメータ表示に代入すると
となり,交点は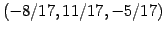 である.
である.
| (176) |
と直線
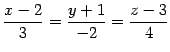 |
(177) |
との交点を考える. 直線の方程式のパラメータ表示は
| (178) |
である.これを平面の方程式に代入すると
| (179) |
より
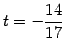 |
(180) |
を得る. 直線の方程式のパラメータ表示に代入すると
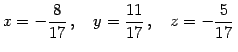 |
(181) |
となり,交点は
Next: 23 点の平面への射影 Up: 1 ベクトルと図形 Previous: 21 平面の方程式 Contents
Kondo Koichi

Created at 2004/11/26