Next: 22 平面と直線の交点 Up: 1 ベクトルと図形 Previous: 20 点と直線との距離 Contents
21 平面の方程式
定義 1.99 (平面)
 空間内の点
空間内の点 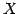 の位置ベクトルが
の位置ベクトルが
と表されるとき, 点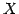 の軌跡を平面(plane)という.
の軌跡を平面(plane)という.
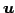 ,
, 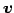 を方向ベクトル(tangent vector)という.
を方向ベクトル(tangent vector)という.
| (148) |
と表されるとき, 点
例 1.100 (平面の具体例)
とおく.このとき平面
を考える. 位置ベクトル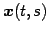 は点
は点 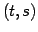 を表す.
を表す.
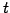 ,
, 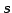 は任意の実数なので
点の軌跡は
は任意の実数なので
点の軌跡は
 空間全体をなす.
よって
空間全体をなす.
よって
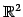 は平面である.
は平面である.
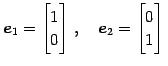 |
(149) |
とおく.このとき平面
 |
(150) |
を考える. 位置ベクトル
例 1.101 (
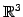 の平面の具体例)
点
の平面の具体例)
点 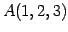 ,
, 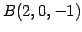 ,
,
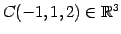 を
通る平面を考える.
点
を
通る平面を考える.
点
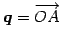 を通り
方向ベクトルが
を通り
方向ベクトルが
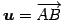 ,
,
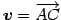 の平面と考える.
の平面と考える.
とする. 平面の方程式のパラメータ表示は
である.
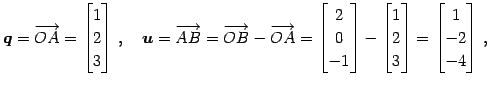 |
(151) | |
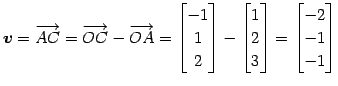 |
(152) |
とする. 平面の方程式のパラメータ表示は
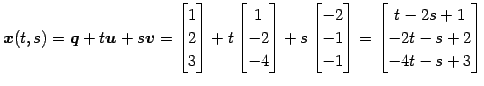 |
(153) |
である.
定理 1.102 (平面の方程式)
 空間内の平面上の点
空間内の平面上の点 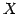 の位置ベクトルは
の位置ベクトルは
と表される. は方向ベクトル
は方向ベクトル 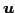 ,
, 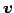 と
直交するベクトルである.
と
直交するベクトルである.
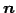 を法線ベクトル(normal vector)という.
を法線ベクトル(normal vector)という.
が成り立つ.
| (154) |
と表される.
(証明)
![]() ,
,
![]() である.
このとき
である.
このとき
| (155) |
が成り立つ.
注意 1.103 (
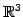 の平面の方程式)
の平面の方程式)
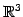 空間内の平面の方程式を考える.
まず,
空間内の平面の方程式を考える.
まず,
とおく.すると方程式
が成り立つ.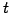 ,
, 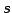 は任意のパラメータであるから消去して方程式とする.
第一式と第二式の
は任意のパラメータであるから消去して方程式とする.
第一式と第二式の 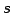 を消去し
を消去し 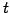 についてまとめると
についてまとめると
が得られる. 他の組合せでも同じ方程式を得る. この方程式は
とおくと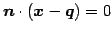 が成り立つ.
また,
が成り立つ.
また,
と表される. さらには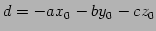 とおいて変形すれば
とおいて変形すれば
である. これらは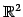 の平面の方程式の成分表示である.
ベクトル
の平面の方程式の成分表示である.
ベクトル 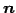 は
は
より,方向ベクトル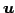 ,
, 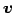 とそれぞれ直交する.
とそれぞれ直交する.
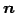 は法線ベクトルである.
また,
ベクトル
は法線ベクトルである.
また,
ベクトル  は
は
 により与えられることに注意する.
により与えられることに注意する.
 |
(156) |
とおく.すると方程式
| (157) |
が成り立つ.
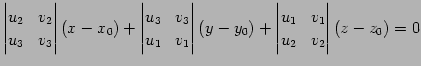 |
(158) |
が得られる. 他の組合せでも同じ方程式を得る. この方程式は
 |
(159) |
とおくと
| (160) |
と表される. さらには
| (161) |
である. これらは
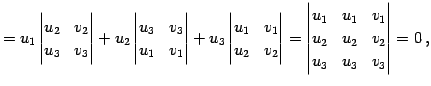 |
(162) | |
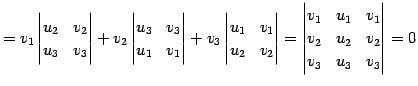 |
(163) |
より,方向ベクトル
例 1.104 (
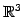 の平面の方程式の具体例)
の平面の方程式の具体例)
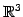 内の平面の方程式
内の平面の方程式
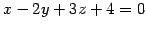 を考える.
法線ベクトルは
を考える.
法線ベクトルは
![$ \vec{n}={[1\,\,\,-2\,\,3]}^{T}$](img746.png) である.
である.
例 1.105 (
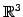 の平面の方程式の具体例)
点
の平面の方程式の具体例)
点  ,
, 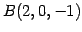 ,
,
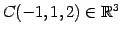 を
通る平面を考える.
点
を
通る平面を考える.
点
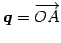 を通り
方向ベクトルが
を通り
方向ベクトルが
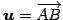 ,
,
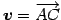 の平面と考える.
の平面と考える.
とする. このとき法線ベクトルは
である. 平面の方程式の成分表示は
より
であるから
を得る.また変形して
を得る.
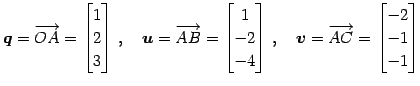 |
(164) |
とする. このとき法線ベクトルは
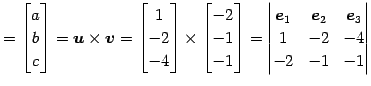 |
(165) | |
 |
(166) |
である. 平面の方程式の成分表示は
| (167) |
より
| (168) |
であるから
| (169) |
を得る.また変形して
| (170) |
を得る.
Next: 22 平面と直線の交点 Up: 1 ベクトルと図形 Previous: 20 点と直線との距離 Contents
Kondo Koichi

Created at 2004/11/26