Next: 21 平面の方程式 Up: 1 ベクトルと図形 Previous: 19 スカラー三重積 Contents
20 点と直線との距離
定義 1.87 (点と直線との距離)
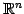 空間内の点
空間内の点 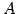 と直線
と直線 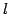 を考える.
点
を考える.
点 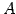 と
と 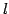 上の点
上の点 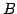 との距離が最小となるとき,
その距離を点と直線との距離という.
との距離が最小となるとき,
その距離を点と直線との距離という.
定理 1.88 (点と直線との距離)
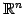 空間内の
点
空間内の
点 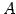 と直線
と直線 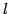 を考える.
点
を考える.
点 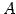 と
と 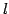 上の点
上の点 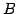 との距離が最小となるのは,
直線
との距離が最小となるのは,
直線 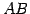 と直線
と直線 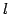 が直交するときである.
が直交するときである.
問 1.89 (点と直線との距離)
これを示せ.
より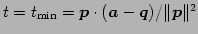 のとき
最小値
のとき
最小値
をとる. このとき
が成り立つ.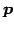 と
と
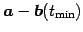 とは直交する.
とは直交する.
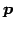 は直線
は直線 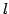 の方向ベクトルであり,
の方向ベクトルであり,
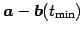 は直線
は直線 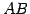 の方向ベクトルである.
よって距離が最小になるとき直線
の方向ベクトルである.
よって距離が最小になるとき直線 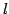 と直線
と直線 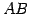 は直交する.
は直交する.
(証明)
点
![]() ,
,
![]() とする.
点
とする.
点 ![]() を直線
を直線 ![]() 上の点とする.
すなわち
上の点とする.
すなわち
![]() とおく.
点
とおく.
点 ![]() と
と ![]() の距離を考える.
の距離を考える.
| (118) | ||
| (119) | ||
| (120) | ||
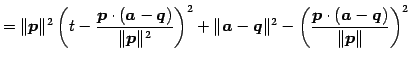 |
(121) |
より
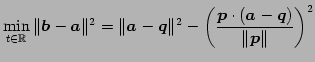 |
(122) |
をとる. このとき
| (123) | ||
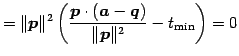 |
(124) |
が成り立つ.
定理 1.90 (点と直線の距離)
 空間内の
点
空間内の
点  と直線
と直線
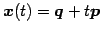 との距離は
との距離は
である.
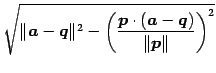 |
(125) |
である.
定理 1.91 (点と直線の距離)
 空間内の
点
空間内の
点  と直線
と直線
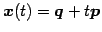 との距離は
との距離は
である.
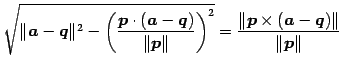 |
(126) |
である.
問 1.92 (
 内の点と直線の距離)
これを示せ.
内の点と直線の距離)
これを示せ.
となる. ここで
を用いると
となり定理を得る.
(証明)
距離
![]() は
は
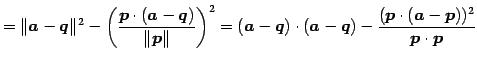 |
(127) | |
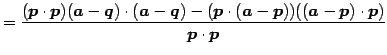 |
(128) |
となる. ここで
| (129) |
を用いると
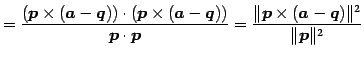 |
(130) |
となり定理を得る.
例 1.93 (
 内の点と直線の距離)
点
内の点と直線の距離)
点  と直線
と直線
![$ \vec{x}(t)={[1\,\,\,3\,\,-1]}^{T}+t{[2\,\,-1\,\,1]}^{T}$](img637.png) との
距離を考える.
点
との
距離を考える.
点 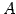 から直線への射影した点を
から直線への射影した点を
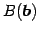 とする.
とする.
であるから,
より,
である.点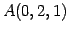 と点
と点
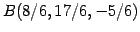 との距離が
点
との距離が
点 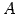 と直線の距離であるから,
と直線の距離であるから,
より
である.
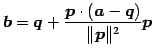 |
(131) |
であるから,
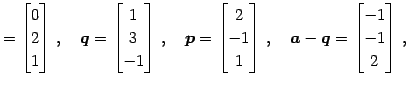 |
(132) | |
| (133) |
より,
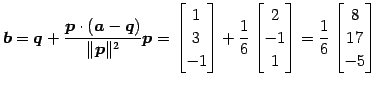 |
(134) |
である.点
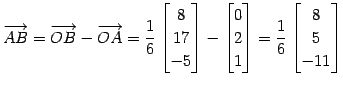 |
(135) |
より
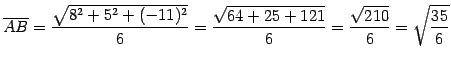 |
(136) |
である.
例 1.94 (
 内の点と直線の距離)
点
内の点と直線の距離)
点 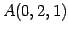 と直線
と直線
![$ \vec{x}(t)={[1\,\,\,3\,\,-1]}^{T}+t{[2\,\,-1\,\,1]}^{T}$](img652.png) との
距離を考える.
との
距離を考える.
であるから,距離は
である.
| (137) |
であるから,距離は
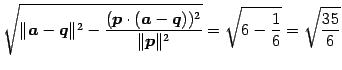 |
(138) |
である.
例 1.95 (
 内の点と直線の距離)
点
内の点と直線の距離)
点 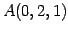 と直線
と直線
![$ \vec{x}(t)={[1\,\,\,3\,\,-1]}^{T}+t{[2\,\,-1\,\,1]}^{T}$](img657.png) との
距離を考える.
との
距離を考える.
より,距離は
である.
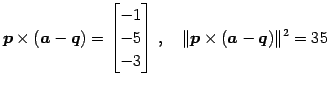 |
(139) |
より,距離は
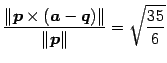 |
(140) |
である.
定理 1.96 (
 内の点と直線の距離)
内の点と直線の距離)
 空間内の点
空間内の点
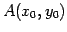 と
直線
と
直線 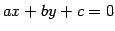 との距離は
との距離は
である.
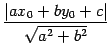 |
(141) |
である.
問 1.97 (
 内の点と直線の距離)
これを示せ.
内の点と直線の距離)
これを示せ.
とおくと
である.よって距離は
である.
(証明)
![]() 空間を
空間を
![]() 空間内の部分空間として考える.
このとき,点
空間内の部分空間として考える.
このとき,点
![]() と直線
と直線
![]() を考える.
を考える.
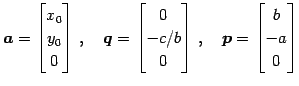 |
(142) |
とおくと
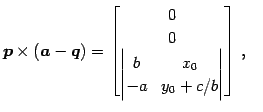 |
(143) | |
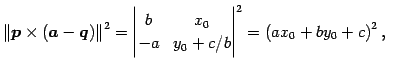 |
(144) | |
| (145) |
である.よって距離は
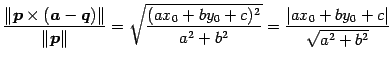 |
(146) |
である.
問 1.98 (
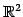 内の点と直線の距離)
点
内の点と直線の距離)
点 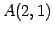 と直線
と直線 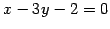 との距離は
との距離は
である.
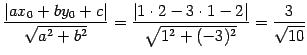 |
(147) |
である.
Next: 21 平面の方程式 Up: 1 ベクトルと図形 Previous: 19 スカラー三重積 Contents
Kondo Koichi

Created at 2004/11/26