3 テイラー級数の導出

巾級数

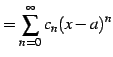$$f(x) = \sum_{n=0}^{\infty}c_{n}(x-a)^{n}$$ (541)

を考える． 関数 $f(x)$ が与えられたとし， テイラー級数の係数 $\{c_{n}\}$ を導出する． $x$ が $a$ に十分近いとき $(x-a)^{n}$ は 次数 $n$ が大きいほど小さくなる． つまり小さい次数の項が主要な項となる． よって小さい次数の係数より順に値を定めて行く．

まず巾級数

$$f(x) =c_{0}+c_{1}(x-a)+c_{2}(x-a)^2+c_{3}(x-a)^3+ c_{4}(x-a)^4+c_{5}(x-a)^5+\cdots$$ (542)

に $x=a$ を代入する．すると

$$f(a) =c_{0}+0+0+\cdots=c_{0}$$ (543)

となる．よって係数を $c_{0}=f(a)$ と定める． 巾級数は

$$f(x) =f(a)+ c_{1}(x-a)+c_{2}(x-a)^2+c_{3}(x-a)^3+ c_{4}(x-a)^4+c_{5}(x-a)^5+\cdots$$ (544)

となる． 両辺を微分すると

$$f'(x) = c_{1}+2c_{2}(x-a)+3c_{3}(x-a)^2+ 4c_{4}(x-a)^3+5c_{5}(x-a)^4+\cdots$$ (545)

を得る．ここに $x=a$ を代入すると

$$f'(a) =c_{1}+0+0+\cdots=c_{1}$$ (546)

となるので係数を $c_{1}=f'(a)$ と定める． このとき巾級数とその導関数は

$$f(x) =f(a)+ f'(a)(x-a)+c_{2}(x-a)^2+c_{3}(x-a)^3+ c_{4}(x-a)^4+c_{5}(x-a)^5+\cdots$$ (547)

$$f'(x) = f'(a)+2c_{2}(x-a)+3c_{3}(x-a)^2+ 4c_{4}(x-a)^3+5c_{5}(x-a)^4+\cdots$$ (548)

となる． これで $1$ 次の項までの係数が定まった． $f(x)$ の最初の二つの項までをみると $x=a$ における接線の方程式となっている． 次に $2$ 階，$3$ 階の導関数と求めて行くと

$$f''(x) = 2\cdot c_{2}+ 3\cdot2\cdot c_{3}(x-a)+ 4\cdot3\cdot c_{4}(x-a)^2+ 5\cdot4\cdot c_{5}(x-a)^3+ \cdots$$ (549)

$$f'''(x) = 3\cdot2\cdot c_{3}+ 4\cdot3\cdot2\cdot c_{4}(x-a)+ 5\cdot4\cdot3\cdot c_{5}(x-a)^2+ \cdots$$ (550)

$$f^{(4)}(x) = 4\cdot3\cdot2\cdot c_{4}+ 5\cdot4\cdot3\cdot2\cdot c_{5}(x-a)+ \cdots$$ (551)

$$f^{(5)}(x) = 5\cdot4\cdot3\cdot2\cdot c_{5}+\cdots$$ (552)

となる．$x=a$ を代入すると

$$f''(a) = 2\cdot c_{2}+0+0+\cdots$$ (553)

$$f'''(a) = 3\cdot2\cdot c_{3}+0+0+\cdots$$ (554)

$$f^{(4)}(a) = 4\cdot3\cdot2\cdot c_{4}+0+0+\cdots$$ (555)

$$f^{(5)}(a) = 5\cdot4\cdot3\cdot2\cdot c_{5}+0+0+\cdots$$ (556)

となるので係数が

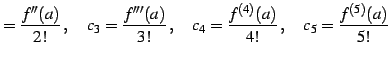$$c_{2} =\frac{f''(a)}{2!}\,,\quad c_{3}=\frac{f'''(a)}{3!}\,,\quad c_{4}=\frac{f^{(4)}(a)}{4!}\,,\quad c_{5}=\frac{f^{(5)}(a)}{5!}$$ (557)

と定まる． 同様な操作を繰り返せば

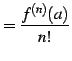$$c_{n} =\frac{f^{(n)}(a)}{n!}$$ (558)

を得る．

Kondo Koichi
Created at 2004/08/14