Next: 9 正項級数の収束性判定法 Up: 4 数列 Previous: 7 級数 Contents
8 正項級数
定義 4.43 (正項級数)
級数
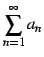 のうち
のうち
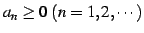 を満たすものを
正項級数(positive term series)と呼ぶ.
を満たすものを
正項級数(positive term series)と呼ぶ.
注意 4.44 (正項級数の単調性)
正項級数
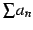 の部分和の数列
の部分和の数列 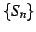 は単調増加である.
は単調増加である.
(証明)
![]() より
より ![]() は広義の単調増加である.
証明終了.
は広義の単調増加である.
証明終了.
定理 4.45 (正項級数の収束定理)
正項級数
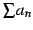 の部分和から得られる数列
の部分和から得られる数列 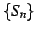 が上に有界なとき,
が上に有界なとき,
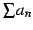 は収束する.
は収束する.
(証明)
![]() は広義の単調増加である.
有界な単調数列は収束するので,
は広義の単調増加である.
有界な単調数列は収束するので,
![]() が上に有界なとき
が上に有界なとき
![]() は収束する.
証明終了.
は収束する.
証明終了.
例 4.46 (正項級数の収束定理の具体例)
正項級数
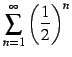 を考える.
部分和は
を考える.
部分和は
となるので
を得る.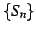 は上に有界である.
よって定理より級数
は上に有界である.
よって定理より級数
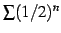 は収束する.
実際,極限を計算すると
前述の例題より
は収束する.
実際,極限を計算すると
前述の例題より
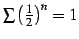 である.
である.
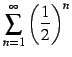 を考える.
部分和は
を考える.
部分和は
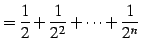 |
(480) | |
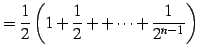 |
(481) | |
| (482) | ||
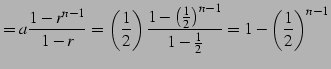 |
(483) |
となるので
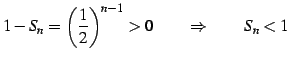 |
(484) |
を得る.
定理 4.47
正項級数
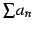 に関して
に関して 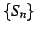 が
有界なとき
が
有界なとき
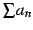 は収束する.
は収束する.
定理 4.48
正項級数
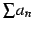 が収束するとき
が収束するとき
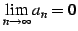 が成り立つ.
が成り立つ.
Kondo Koichi

Created at 2004/08/14