Next: 10 交項級数 Up: 4 数列 Previous: 8 正項級数 Contents
9 正項級数の収束性判定法
定理 4.49 (比較判定法)
二つの正項級数
を考える. 数列 ,
, 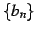 がある正の整数
がある正の整数 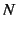 に対して
に対して
を満たすとき, 次の関係が成り立つ:
 |
(485) |
を考える. 数列
| (486) |
を満たすとき, 次の関係が成り立つ:
- (i)
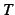 が収束するとき,
が収束するとき,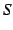 も収束する.
も収束する.
- (ii)
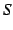 が発散するとき,
が発散するとき,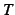 も発散する.
も発散する.
例 4.50 (比較判定法の具体例)
級数
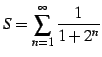 を考える.
数列
を考える.
数列
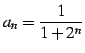 ,
,
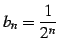 とする.
このとき
とする.
このとき
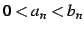 を満たす.
また,級数
を満たす.
また,級数
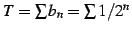 は収束する.
よって定理より級数
は収束する.
よって定理より級数
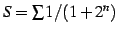 もまた収束する.
もまた収束する.
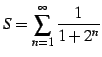 を考える.
数列
を考える.
数列
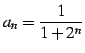 ,
,
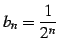 とする.
このとき
とする.
このとき
定理 4.51 (比較判定法)
二つの正項級数
を考える. 数列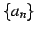 ,
, 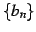 が
が
を満たし,かつ級数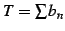 が収束するとき,
級数
が収束するとき,
級数
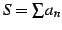 も収束する.
も収束する.
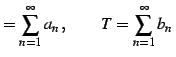 |
(487) |
を考える. 数列
| (488) |
を満たし,かつ級数
例 4.52 (調和級数)
級数
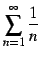 を
調和級数(harmonic series)という.
調和級数は発散する.
を
調和級数(harmonic series)という.
調和級数は発散する.
の各項を括り直して
と考える.ここで は
は
であり,
とおいている. を満たす
を満たす 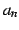 をさがす.
をさがす.
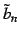 に関して不等式
に関して不等式
が成り立つので,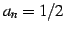 とおけば
とおけば
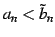 を得る.
よって比較判定法より
を得る.
よって比較判定法より
を得る.以上証明終り.
(証明)調和級数
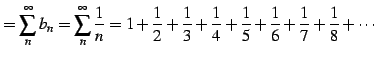 |
(489) |
の各項を括り直して
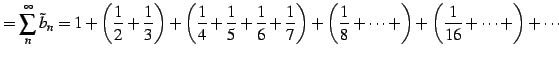 |
(490) |
と考える.ここで
| (491) | ||
 |
(492) | |
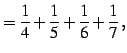 |
(493) | |
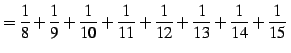 |
(494) |
であり,
 |
(495) |
とおいている.
 |
(496) | |
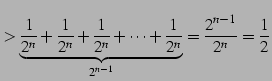 |
(497) |
が成り立つので,
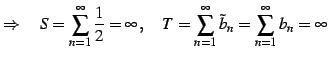 |
(498) |
を得る.以上証明終り.
定理 4.53 (ダランベールの収束判定法)
正項級数
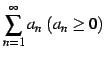 は,
極限
は,
極限
により,級数の収束性の判定ができる:
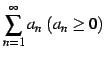 は,
極限
は,
極限
| (499) |
により,級数の収束性の判定ができる:
- (i)
 のとき,
のとき,
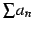 は収束する.
は収束する.
- (ii)
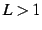 のとき,
のとき,
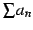 は発散する.
は発散する.
- (iii)
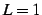 のとき,
のとき,
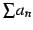 の収束性は判定できない.
の収束性は判定できない.
例 4.54 (ダランベールの判定法の具体例)
級数
を考える.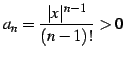 であるから,
であるから,
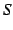 は正項級数である.
よって
は正項級数である.
よって
が成り立つので,ダランベールの判定法より級数は収束する.
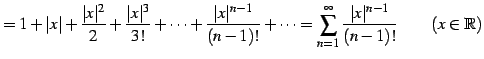 |
(500) |
を考える.
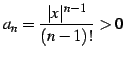 であるから,
であるから,
 |
(501) |
が成り立つので,ダランベールの判定法より級数は収束する.
例 4.55 (ダランベールの判定法で判定できない例)
調和級数
 を考える.
隣り合う項の比の極限は
を考える.
隣り合う項の比の極限は
となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う.
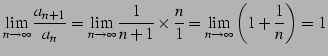 |
(502) |
となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う.
問 4.56
参考書(p.180)問題7-3.
定理 4.57 (コーシーの収束判定法)
正項級数
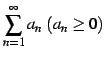 は,
極限
は,
極限
により,級数の収束性の判定ができる:
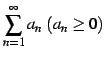 は,
極限
は,
極限
| (503) |
により,級数の収束性の判定ができる:
- (i)
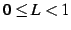 のとき,
のとき,
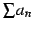 は収束する.
は収束する.
- (ii)
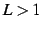 のとき,
のとき,
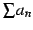 は発散する.
は発散する.
- (iii)
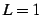 のとき,
のとき,
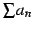 の収束性は判定できない.
の収束性は判定できない.
Next: 10 交項級数 Up: 4 数列 Previous: 8 正項級数 Contents
Kondo Koichi

Created at 2004/08/14