Next: 8 正項級数 Up: 4 数列 Previous: 6 数列の有界性と単調性 Contents
7 級数
級数(series)とは数列 ![]() の和である.
式では
の和である.
式では
| (427) | ||
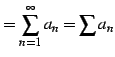 |
(428) |
と書き表す. 加法(足し算)は有限回の演算においてのみ定義されているので, 式(
| (429) |
を考える. これを第
| (430) |
を考える. 数列
| (431) |
が存在したとする. このとき級数
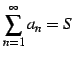 |
(432) |
で与えられると定義する. 極限
定義 4.30 (級数)
数列 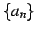 の和
の和
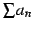 を級数(series)と呼び,
その値は
を級数(series)と呼び,
その値は
で定義する. この極限が存在するとき 級数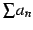 は収束する(convergent)といい,
収束しない場合を
級数
は収束する(convergent)といい,
収束しない場合を
級数
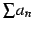 は発散する(divergent)という.
は発散する(divergent)という.
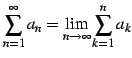 |
(433) |
で定義する. この極限が存在するとき 級数
例 4.33 (無限級数の結合則)
数列
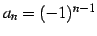 の
級数
の
級数
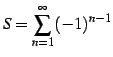 を考える.
すなわち
を考える.
すなわち
である. 足し算の順を入れ替えると
となる.また別の順で足し合わせると
となる. これらは矛盾する. どこが誤りであろうか? 有限の項の和の常識は無限の項の和には通用しない. この場合の間違いは足し算の順を変えたことである. この例では結合則が成り立たない. 定義![[*]](./icons/crossref.png) に従えば級数
に従えば級数 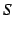 は発散である.
は発散である.
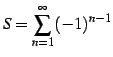 を考える.
すなわち
を考える.
すなわち
| (435) |
である. 足し算の順を入れ替えると
| (436) | ||
| (437) |
となる.また別の順で足し合わせると
| (438) | ||
| (439) |
となる. これらは矛盾する. どこが誤りであろうか? 有限の項の和の常識は無限の項の和には通用しない. この場合の間違いは足し算の順を変えたことである. この例では結合則が成り立たない. 定義
例 4.34 (等比級数)
等比数列
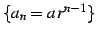 の無限和を
等比級数(geometrical progression series)と呼び,
の無限和を
等比級数(geometrical progression series)と呼び,
と書き表す. 等比級数は
となる.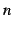 部分和
部分和
を考える.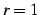 のとき,
のとき,
となる. つぎに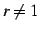 のとき,等式
のとき,等式
を用いると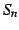 は
は
と書ける. 以上より
となる. ただし無限大の符号は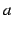 の符号
の符号
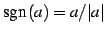 で決まる.
証明終り.
で決まる.
証明終り.
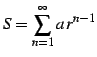 |
(440) |
と書き表す. 等比級数は
![$\displaystyle S=\left\{ \begin{array}{ll} \displaystyle{\frac{a}{1-r}} & (\vert r\vert< 1) \\ [1em] \text{発散} & (\vert r\vert\ge 1) \end{array} \right.$](img1491.png) |
(441) |
となる.
(証明) 第
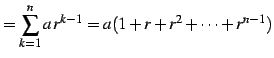 |
(442) |
を考える.
| (443) |
となる. つぎに
| (444) |
を用いると
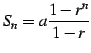 |
(445) |
と書ける. 以上より
![$\displaystyle S=\lim_{n\to\infty}S_{n}= \left\{ \begin{array}{lc} \displaystyle...
...& (-1<r<1)\\ [2ex] \displaystyle{\text{不確定}} & (r\leq-1) \end{array} \right.$](img1501.png) |
(446) |
となる. ただし無限大の符号は
問 4.35 (1を根にもつ多項式の因数分解)
次の等式を示せ.
| (447) |
注意 4.36 (初項が異なる級数)
級数が
と定義されるときの値を考える. 部分和は
となるから, 結局級数は
と得られる.
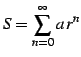 |
(448) |
と定義されるときの値を考える. 部分和は
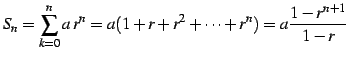 |
(449) |
となるから, 結局級数は
![$\displaystyle S= \lim_{n\to\infty}S_{n}= \lim_{n\to\infty}a\frac{1-r^{n+1}}{1-r...
...(\vert r\vert<1) \\ [1ex] \text{発散} & (\vert r\vert\geq1) \end{array} \right.$](img1507.png) |
(450) |
と得られる.
注意 4.37 (等比級数の有理式表現)
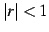 のとき
のとき
とな. この式は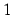 を
を 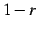 で割ることでも導出される.
すなわち,
で割ることでも導出される.
すなわち,
のように低次項を主項として割り算を無限回続ける.
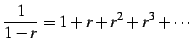 |
(451) |
とな. この式は
| (452) | ||
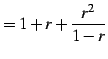 |
(453) | |
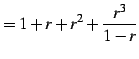 |
(454) | |
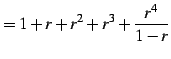 |
(455) | |
| (456) |
のように低次項を主項として割り算を無限回続ける.
例 4.38 (等比級数の具体例)
または
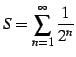 |
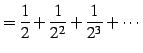 |
(457) |
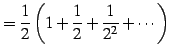 |
(458) | |
| (459) | ||
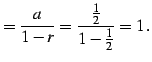 |
(460) |
または
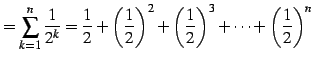 |
(461) | |
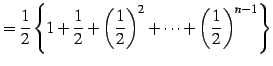 |
(462) | |
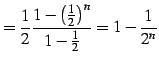 |
(463) |
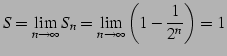 |
(464) |
例 4.39 (等比級数の具体例)
または
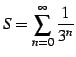 |
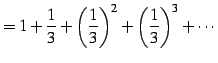 |
(465) |
| (466) | ||
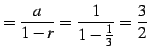 |
(467) |
または
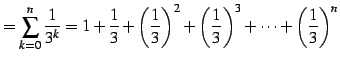 |
(468) | |
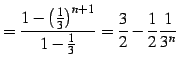 |
(469) |
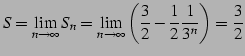 |
(470) |
例 4.40 (等比級数の具体例)
| (471) |
(証明)
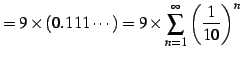 |
(472) | |
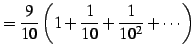 |
(473) | |
| (474) | ||
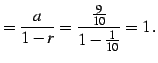 |
(475) |
問 4.41
参考書(p.172)問題7-1.
問 4.42 (級数の計算)
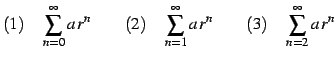 |
(476) | |
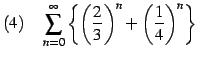 |
(477) | |
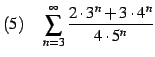 |
(478) | |
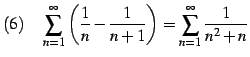 |
(479) |
Next: 8 正項級数 Up: 4 数列 Previous: 6 数列の有界性と単調性 Contents
Kondo Koichi

Created at 2004/08/14