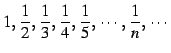Next: 3 発散する数列のいろいろ Up: 4 数列 Previous: 1 数列 Contents
2 数列の極限
数列と与えられたとする. この数列
定義 4.6 (数列の極限)
収束しない場合を発散する(divergent)という.
| (373) | ||
| |
(374) | |
| (375) | ||
| (376) | ||
| (377) | ||
| (378) |
収束しない場合を発散する(divergent)という.
注意 4.7 (数列の極限に関する注意)
数列(![[*]](./icons/crossref.png) )は
)は
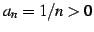 であるので,
であるので,
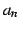 がいかに 0 に近づいたとしても,
決して 0 になることはない.
がいかに 0 に近づいたとしても,
決して 0 になることはない.
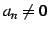 である.
である.
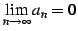 の意味はあくまでも,
数列
の意味はあくまでも,
数列 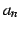 は 0 に近づいて行く,という意味である.
は 0 に近づいて行く,という意味である.
例 4.8 (負巾で表される数列の極限)
次の一般項をもつ数列をそれぞれ考える:
すべての数列に対して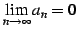 である.
これは標語的に書くと
である.
これは標語的に書くと
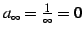 である.
このとき数列は有限確定である.
である.
このとき数列は有限確定である.
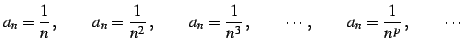 |
(379) |
すべての数列に対して
Kondo Koichi

Created at 2004/08/14