Next: 4 数列の極限に関する定理 Up: 4 数列 Previous: 2 数列の極限 Contents
3 発散する数列のいろいろ
例 4.9 (プラス無限大に無限確定な数列)
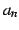 はプラス無限大(
はプラス無限大(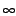 )に発散する.
)に発散する.
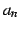 は無限確定である.
は無限確定である.
| (380) |
| (381) |
例 4.10 (マイナス無限大に無限確定な数列)
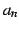 はマイナス無限大(
はマイナス無限大( )に発散する.
)に発散する.
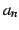 は無限確定である.
は無限確定である.
| (382) |
| (383) |
例 4.11 (有限不確定な数列)
有限な値に確定しないので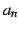 は発散する.
は発散する.
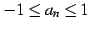 が成立している.
が成立している.
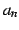 は有限の範囲内に押さえられ振動的な
ふるまいをする.
は有限の範囲内に押さえられ振動的な
ふるまいをする.
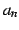 は有限不確定である.
は有限不確定である.
| (384) |
| (385) |
有限な値に確定しないので
例 4.12 (無限不確定な数列)
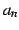 は有限な値に確定しない.
は有限な値に確定しない. 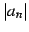 は増大して行く.
ゆえに
は増大して行く.
ゆえに 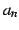 は無限不確定である.
は無限不確定である.
| (386) |
| (387) |
Next: 4 数列の極限に関する定理 Up: 4 数列 Previous: 2 数列の極限 Contents
Kondo Koichi

Created at 2004/08/14