Next: 2 テイラー級数 Up: 4 テイラー級数 Previous: 4 テイラー級数 Contents
1 巾級数
定義 4.1 (巾級数)
定数
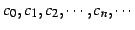 と
変数
と
変数 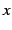 を考える.
このとき級数
を考える.
このとき級数
を巾級数(power series)または 整級数(polynomial series)と呼ぶ. 同様に級数
を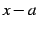 の巾級数と呼ぶ.
の巾級数と呼ぶ.
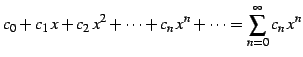 |
(502) |
を巾級数(power series)または 整級数(polynomial series)と呼ぶ. 同様に級数
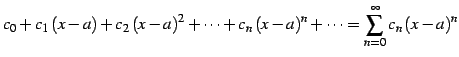 |
(503) |
を
定義 4.2 (収束半径)
巾級数
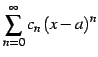 は
は
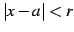 のとき絶対収束し,
のとき絶対収束し,
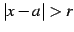 のとき発散する.
定数
のとき発散する.
定数 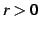 を収束半径(radius of convergence)と呼ぶ.
を収束半径(radius of convergence)と呼ぶ.
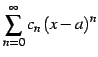 は
は
例 4.3 (収束半径の具体例)
巾級数
は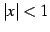 のとき収束する(公比が
のとき収束する(公比が 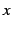 の等比級数であるから).
よって収束半径は
の等比級数であるから).
よって収束半径は 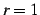 である.
である.
は任意の有限の実数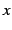 に対して収束する(例題
に対して収束する(例題 ![[*]](./icons/crossref.png) ).
すなわち
).
すなわち
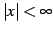 において収束する.
このとき収束半径は
において収束する.
このとき収束半径は 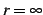 と表わす.
と表わす.
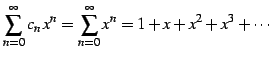 |
(504) |
は
巾級数
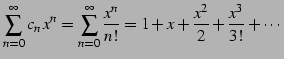 |
(505) |
は任意の有限の実数
定理 4.4 (収束半径の計算法)
巾級数
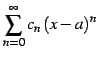 を考える.
極限
を考える.
極限
または
が存在するとき, 巾級数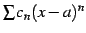 の収束半径は
の収束半径は 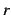 である.
である.
であるので,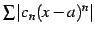 が収束するとき
が収束するとき
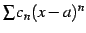 も収束する.
も収束する.
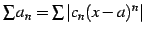 とおくと,
とおくと,
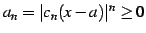 であるから
であるから
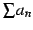 は正項級数となる.
ゆえにダランベールの
収束判定法(定理
は正項級数となる.
ゆえにダランベールの
収束判定法(定理 ![[*]](./icons/crossref.png) )より,
級数
)より,
級数
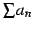 は
は
のとき収束する. よって
となる. これより
を得る. 以上より収束半径は
と求まる. 同様にしてコーシーの 収束判定法(定理![[*]](./icons/crossref.png) )より
)より
![$ \displaystyle{r=\lim_{n\to\infty}1/\sqrt[n]{\vert c_{n}\vert}}$](img1686.png) が求まる.
が求まる.
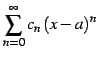 を考える.
極限
を考える.
極限
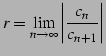 |
(506) |
または
![$\displaystyle r=\lim_{n\to\infty} \frac{1}{\sqrt[n]{\vert c_{n}\vert}}$](img1667.png) |
(507) |
が存在するとき, 巾級数
(証明)
級数
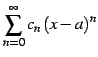 と
その絶対級数
と
その絶対級数
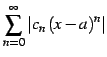 を
考える.
このとき
を
考える.
このとき
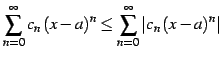 |
(508) |
であるので,
| (509) |
のとき収束する. よって
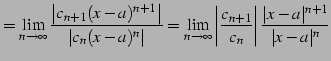 |
(510) | |
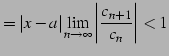 |
(511) |
となる. これより
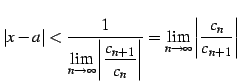 |
(512) |
を得る. 以上より収束半径は
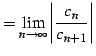 |
(513) |
と求まる. 同様にしてコーシーの 収束判定法(定理
例 4.5 (収束半径の計算例)
巾級数
の収束半径を求める.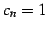 であるから,収束半径は
であるから,収束半径は
と求まる. 巾級数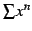 は
は
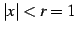 のとき収束し,
のとき収束し,
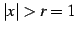 のとき発散する.
のとき発散する.
の収束半径を求める.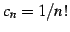 であるから,収束半径は
であるから,収束半径は
と求まる.収束半径は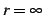 である.
巾級数
である.
巾級数
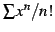 は任意の実数
は任意の実数 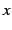 に対して収束する.
に対して収束する.
の収束半径を求める.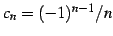 であるから,
収束半径は
であるから,
収束半径は
と求まる. 巾級数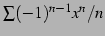 は
は
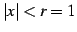 のとき収束し,
のとき収束し,
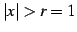 のとき発散する.
のとき発散する.
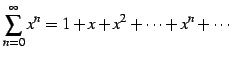 |
(514) |
の収束半径を求める.
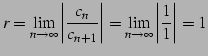 |
(515) |
と求まる. 巾級数
巾級数
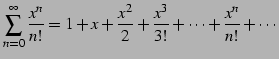 |
(516) |
の収束半径を求める.
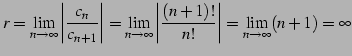 |
(517) |
と求まる.収束半径は
巾級数
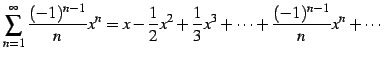 |
(518) |
の収束半径を求める.
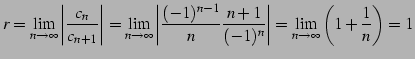 |
(519) |
と求まる. 巾級数
問 4.6
参考書(p.191)問題7-5 1.
Next: 2 テイラー級数 Up: 4 テイラー級数 Previous: 4 テイラー級数 Contents
Kondo Koichi
Created at 2003/08/29